Olademo J. O.;1 & Akinmuyise M. F.2
1Adeyemi Federal University of Education, Ondo State, Nigeria
*Corresponding Author Email: olademojo@aceondo.edu.ng …
Highlights
Abstract
The teaching and learning of Mathematics should ideally progress through three stages: starting from Concrete, to Pictorial, and finally, to Abstract concepts. This paper specifically highlights the concrete and pictorial stages in the teaching and learning process of certain square-related mathematical identities such as (a+b)2, a2-b2 and (a-b)2. This approach allows learners to conceptualize Mathematics in a tangible form before proceeding to abstract generalizations. The formulas mentioned were derived from geometrical representations of squares in various configurations. The findings of this approach were then juxtaposed with traditional formulas, which typically lack a geometric foundation and are understood through algebraic manipulation, such as expansion (i.e., simplifying expressions by removing brackets). Employing geometry not only enriches students’ understanding but also enables them to derive these results more intuitively, even without prior knowledge of algebraic bracket expansion techniques. This method underscores the significance of visual and spatial reasoning in grasping mathematical concepts, providing a solid foundation for further mathematical abstraction and reasoning.
Keywords: Mathematical Identities, Figure, Concrete, Pictorial, Abstract, Expansion.
1. Introduction
This paper explores the utilization of squares and triangles to demystify mathematical identities, thereby rendering mathematics more tangible and less abstract. This practical orientation of mathematics proves significantly beneficial in real-world applications such as land measurement, building, and road construction.
Borishade (2002) emphasized that measuring area involves determining the surface coverage of a shape.
Joarder (2015) stated that

He further that it is interesting to note that the first term a2 in the left hand side of the equation 1a is the area of a square with each side of a units, the second term 2ab is linear in a and is the areas of the twin rectangles (rectangles having the same area) with sides of a and b units, and the third term is the area of a square with each side of b units.
Swan and Marshall (2010) and Ponte et al. (2023) advocated for enhancing student engagement in their learning process by employing manipulative materials, which foster observation, exploration, and reflection, thereby aiding in the organization of thought and conceptual structuring.
Steffe and Thompson (2000) highlighted that the formulation of concepts in mathematics is deeply rooted in experience, suggesting that abstract thinking can evolve from experimental learning.
Kalejaiye et al. (2011) defined a square as a rectangle with equal side lengths and right angles. This work further illuminates the geometry of everyday objects, inspiring creativity. It also considers the areas of such squares as part of the illustrative process. The manipulation of mathematical concepts through tangible means is pivotal for meaningful learning, as it aids in developing visualization skills grounded in concrete experiences and the exploration of various geometric forms.
2. Geometrical Illustration of the Mathematics Identities of Interest
Mathematics identities to be illustrated here include:
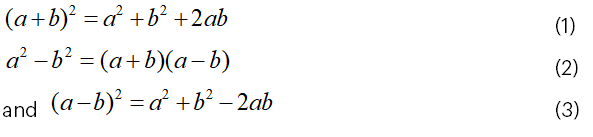
2.1 Geometrical Representation of the Identity

2.1.1 An Existing Method
Gittleman (1972) used a square of side a+b, and after partitioning into four reasonable areas, got the result by actually expanding or opening the brackets.
The figure below is a square of side a+b.
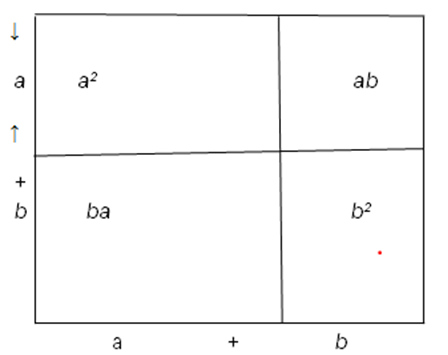
The square consists of four components with areas a2, b2, ab and ba.
Since the same square is partitioned into the four areas, then the area of the large square must be equal to the sum of the area of those four smaller parts.
Thus, (a+b)(a+b)=a2+ b2+ab+ba
Or (a+b)2=a2+ b2+2ab (since ab = ba)
2.1.2 The Developed Method Using Right-Angled Isosceles
There are at least two triangles in a square.
Draw an isosceles triangle whose equal sides are a+b as shown below

In the figure above, there are three right angled triangles and a rectangle of side
Length b and base a.
Area of triangle = ½(a+b)(a+b) or ½(a+b)2.
The original triangle has three component areas ½a2, ½b2 and ab
Since the same triangle is partitioned, then the areas must be equal.
i.e. ½(a+b)2 = ½a2+ ½b2 + ab (2.1)
Multiply both side of equation (2.1) by 2 to get
i.e. (a+b)2 = a2+ b2 + 2ab
2.1.4 Geometrical Representation of the Identity
a2-b2= (a-b) (a+b)
An Existing Method
In elementary algebra, the identity a2– b2= (a-b) (a+b) is referred to as the Difference of Two Squares, or the Difference of Perfect Squares. This implies that a squared number subtracted from another squared number.
Coolidge (1963) emphasized that the mathematical concept of the difference of two squares can be visualized geometrically as the difference between the areas of two squares on a plane. To illustrate this, consider a diagram where the shaded region highlights the area difference between two squares, denoted as (a-b)
In the diagram, the area of the shaded part can be found by adding the areas of the two rectangles. The shaded portion represents the difference between the areas of the two squares. a(a-b) +b(a-b)
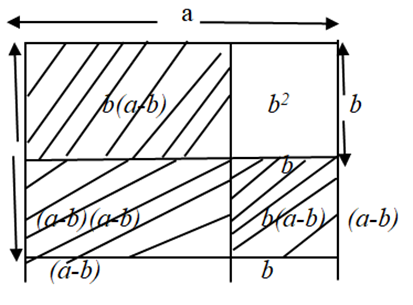
The area of the whole square with side a is the sum of the areas of the four components. That is a2= b(a-b)+(a-b)(a-b)+ b(a-b) +b2
a2–b2= b(a-b) + (a-b)(a-b) + b(a-b)
a2–b2=(a-b) (a-b+b+b+b)
This leads to (a+b)(a-b)
Thus, a2–b2=(a-b)(a+b)
2.15 The Developed Method Using Triangle

Consider an isosceles right-angled triangle of side a, as shown above.
The area of this triangle is ½axa=½a2.
The triangle is partitioned into three components whose areas are
½b2, b(a-b) and ½(a-b)(a-b).
Since the original triangle is the same as the partitioned, they have equal areas.

Multiply through by 2 to get
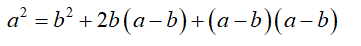
Expansion and simplification give

Geometrical Representation of the Identity
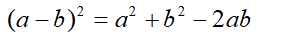
An Existing Method
According to Gittleman (1972), the Babylonians knew the formula (a-b)2=a2+b2-2ab by means of geometrical diagram.
According to Gittleman (1972), the Babylonians knew the formula (a-b)2=a2+b2-2ab by means of geometrical diagram.
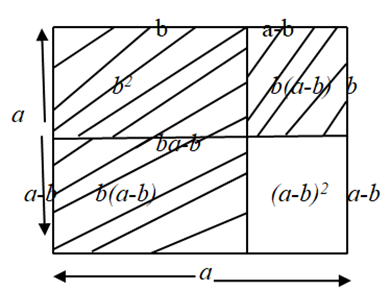
Consider a square of side a.
Let another smaller square of side b be partitioned from the original square.
The unshaded portion represents an area covered by (a-b)(a-b) or (a-b)2.
Now shaded area is b2+ b(a-b) + b(a-b).
Hence, we have (a-b)2 = a2-{b2+2b(a-b)} or (a-b)2 = a2-b2+ 2b(a-b) = a2-b2+ 2b2 – 2ab = a2+ b2– 2ab
3. Methodology
3.1 The Developed Method Using Triangle
Below is a isosceles right angled triangle of side a
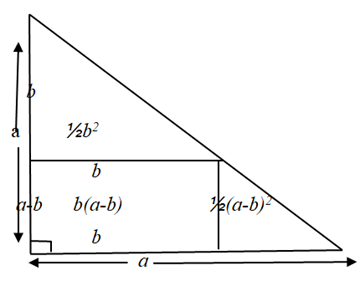
The area of this triangle is ½axa =½ a2
The triangle is partitioned into three portions whose areas are ½b2, b(a-b) and ½(a-b)(a-b).
Thus, we must have that ½ a2 = ½(a-b)2+ ½b2 +b(a-b).
= ½(a-b)2 -½b2 +ab
This leads to ½(a-b)2= ½a2+½b2-ab
or (a-b)2= a2 b2-2ab
4. Conclusion
Geometrical problems of the type discussed can be effectively simplified into terms or components. At a subsequent stage, the solution construction primarily necessitates knowledge of the lengths of specific straight lines or the areas of designated regions. The concept of the difference of two squares plays a crucial role in the factorization of expressions, including finding the linear factors of the sum of two squares through the use of complex number coefficients. This technique not only streamlines the process of solving geometrical challenges but also enriches our understanding and application of algebraic principles in geometry e.g. finding linear factors of z2 + 5.
To enhance the effectiveness of teaching and learning in mathematics, it is essential to progress from concrete examples to pictorial representations, and finally to abstract concepts. Employing diagrams to illustrate mathematical ideas, formulas, or identities renders the subject more tangible and less abstract, making mathematics more relatable and understandable for learners. This approach facilitates a deeper comprehension of mathematical principles by grounding them in real-world contexts before transitioning to their abstract formulations.
The challenge ahead of the writers and the readers is illustrating the identity (a+b)3 = a3+3a2b + 3ab2+b3 using a cube of side (a+b).
We must make a trial!
Conflict of Interest
There is no conflict of interest during the completion of the research.
References
Borishade, A. B. (2002). National Teachers Grade Two Certificate Course Book on Mathematics (pp. 89-91). National Teachers Institute, Kaduna.
Coolidge, J. L. (1963). A history of geometrical methods. Dover Publications.
Gittleman, A. (1972). History of mathematics. Merrill Publishing Company.
Joarder, A. H. (2015). Factorization with geometric insights. The Australian Association of Mathematics Journal, 29(1), 25-30.
Kalejaiye, A. O., et al. (2011). New general mathematics for West Africa (Senior Secondary I). Pearson Education Limited.
Ponte, R., Viseu, F., Neto, T., & Aires, A. P. (2023). Revisiting manipulatives in the learning of geometric figures. Journal of Teacher Education, 8. https://doi.org/10.3389/feduc.2023.1217680
Steffe, L. P., & Thompson, P. W. (2000). Teaching experiment methodology: Underlying principles and essential elements. In R. Lesh & A. E. Kelly (Eds.), Research design in mathematics and science education (pp. 267-307). Erlbaum.
Swan, P., & Marshall, L. M. (2010). Revisiting mathematics manipulative materials. Journal Name Missing, 13, 13-19.
About this Article
Cite this Article
APA
OlademoJ. O. & Akinmuyise M. F. (2024). Determination of Some Selected Mathematical Identities Using Triangular Method-An improvement over existing method. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.
Chicago
OlademoJ. O. & Akinmuyise M. F. 2024. “Determination of Some Selected Mathematical Identities Using Triangular Method-An improvement over existing method.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.
Received
22 November 2023
Accepted
12 February 2024
Published
26 February 2024
Corresponding Author Email: olademojo@aceondo.edu.ng
Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.
Distributed under Creative Commons CC-BY 4.0
Share this article
Use the buttons below to share the article on desired platforms.