Green Mathematics: Harnessing Mathematical Models for Sustainable Resource Management

Adenike A. Akinsemolu¹

¹Adeyemi Federal University of Education, Ondo State, Nigeria

*Corresponding Author Email: akinsemoluaa@aceondo.edu.ng …

Read More

Highlights

Abstract

This chapter explores the vital role of Green Mathematics in advancing sustainable resource management within the broader context of environmental science. Mathematical models are essential tools that translate complex ecological dynamics into manageable, quantitative assessments, enabling more effective decision-making for sustainability. This work delineates the theoretical foundations of mathematical modelling, addressing how differential equations, statistical methods, and computational tools can aid in the understanding and management of natural systems. It then showcases diverse applications across key areas such as renewable energy optimization, water resource management, and wildlife conservation, illustrated through in-depth case studies from various global contexts. These include water management strategies in California, renewable energy optimization in Germany, and agricultural sustainability practices in Ethiopia. Despite their extensive applications, mathematical models face significant challenges, including data limitations, complexity of natural systems, and the need for model validation. The chapter concludes by discussing future directions in Green Mathematics, highlighting the integration of big data, real-time analytics, and enhanced model interoperability as prospects for addressing current limitations and expanding the capacity of mathematical models to support global sustainability efforts. This discussion not only underscores the importance of mathematical approaches in environmental management but also aligns with the interdisciplinary nature of the book Exploring STEM Frontiers, emphasizing the critical role of STEM in tackling environmental challenges.

Keywords: Sustainable Resource Management; Mathematical Modelling; Environmental Science; Green Mathematics; Computational Tools.

1. Introduction

1.1 The Emergence of Green Mathematics

In the age of unprecedented environmental challenges, the role of mathematics as a tool for sustainability has never been more crucial (Rehmeyer et al., 2011). The concept of “Green Mathematics” is not merely an academic discipline; it represents a vital approach in leveraging quantitative methods to address and mitigate environmental issues (Barwell, 2018). This chapter aims to explore the intersection of mathematics and environmental science, particularly focusing on how mathematical models are applied in sustainable resource management.

1.2 The Vital Role of Mathematical Models

Mathematical models serve as foundational tools in understanding complex natural systems and formulating strategies for their management (Zeidan, 2017). By abstracting real-world processes into mathematical terms, these models allow scientists, policymakers, and researchers to simulate scenarios, predict outcomes, and make informed decisions about resource allocation, conservation efforts, and environmental protection. These models are crucial for planning sustainable futures in various sectors, including agriculture, water management, energy, and biodiversity conservation (Billionnet 2013; Liu et al., 2013; Mellaku & Sebsibe, 2022).

1.3 Objectives of the Chapter

The primary objective of this chapter is to articulate the significance of mathematical models in the field of sustainability. It aims to:

1. Explain the theoretical underpinnings of mathematical modelling related to environmental systems.
2. Showcase the diverse applications of these models in managing natural resources effectively and sustainably.
3. Highlight successful case studies where mathematical models have significantly contributed to environmental management and policy.
4. Discuss the inherent challenges and limitations faced in modelling environmental systems.
5. Explore future directions for Green Mathematics, focusing on emerging trends and technologies that could shape the next generation of environmental modelling.

By providing a comprehensive overview of Green Mathematics, this chapter will contribute to the broader discourse on sustainable resource management within the context of the book Exploring STEM Frontiers. The ensuing sections will explore deeper into the mathematical methodologies and their practical applications, illustrating how they can be harnessed to foster a more sustainable world.

2. Theoretical Foundations of Mathematical Modelling in Sustainability

2.1 Basic Principles of Mathematical Modelling

Mathematical modelling in the context of environmental science involves the translation of natural phenomena into mathematical language (Zeidan, 2017). This process enables researchers to simplify complex ecosystems and environmental processes into manageable and quantifiable components. By establishing relationships between variables and constants, models can predict outcomes, simulate potential future scenarios, and provide a basis for sound decision-making (Li et al., 2013; Mbagwu et al., 2021).

The core of mathematical modelling for sustainability lies in the ability to use equations and algorithms to mirror real-world dynamics (Kundu, 2018). For instance, differential equations are widely used to model the rate of change in populations, pollution levels, or resource depletion over time. Statistical models, on the other hand, help in analyzing variability and trends within environmental data, providing insights that are critical for effective management strategies.

2.2 Key Mathematical Tools and Methods

To understand the application of mathematical modelling in sustainability, it is essential to explore some of the key tools and methods in more depth. This includes not only a description of these tools but also examples of typical equations and models used in environmental studies.

2.2.1 Differential Equations

Differential equations are a cornerstone in modelling continuous processes within environmental systems (Zhao et al., 2024). These equations describe how a particular variable evolves over time, dependent on its current state and rate of change.

Example
Consider a simple model of a fish population (𝑡)P(t) in a lake, which is subject to natural growth and harvesting. The rate of change of the population can be modeled by the differential equation:

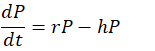
Here, 𝑟 represents the natural growth rate of the fish population, and ℎ represents the rate of harvesting. This model helps in predicting the sustainability of the fish population over time, guiding harvesting policies to avoid overfishing.

2.2.2 Statistical Models

Statistical models are invaluable for analyzing environmental data, particularly when dealing with variability and uncertainty (Filipsson, 2011). These models can predict trends and assess the impact of different variables on environmental outcomes.

Example
A linear regression model might be used to predict air pollution levels based on traffic volume and industrial activity. The model could be represented as:
Y = β₀   + β₁X₁ + β₂X₂ + ϵ

where 𝑌 is the pollution level, X₁​ is traffic volume, 𝑋₂ is industrial activity, 𝛽₀, 𝛽₁ ,𝛽₂​ are parameters to be estimated, and 𝜖 is the error term, representing unexplained variability.

2.2.3 Optimization Models

Optimization models are designed to identify the most effective solutions under given constraints, which is crucial for resource allocation and management (IBM, 2024).

Example
An optimization model for water resource management might involve allocating water among agricultural, industrial, and residential users to maximize efficiency while minimizing waste. The model could use a linear programming approach:

Maximize Z = c₁​x₁ ​+ c₂​x₂ ​+ c₃​x_3​

subject to:
a₁₁​x₁ ​+ a₁₂​x₂ + a₁₃​x₃ ​≤ b₁​
𝑎₂₁𝑥₁ + 𝑎₂₂𝑥₂ + 𝑎₂₃𝑥₃ ≤ 𝑏₂
𝑥₁, 𝑥₂, 𝑥₃ ≥ 0

where 𝑥₁,𝑥₂,𝑥₃ are the amounts of water allocated to each user type, 𝑐₁,𝑐₂,𝑐₃ are the benefits of water to each user, and 𝑎𝑖𝑗​ and 𝑏𝑖​ represent the constraints on water usage.

2.2.4 Computational Models

As environmental challenges become more complex, computational models play a crucial role in synthesizing data and simulating intricate processes across multiple scales (Pianosi, 2014).

Example
A computational model for climate change might integrate various data inputs like temperature, CO2 levels, ocean currents, and solar radiation to predict global temperature changes and weather patterns. The model might use complex algorithms to solve a series of differential equations that represent the Earth’s climate systems.

2.3 Bridging Theory and Practice

While the theoretical foundations provide the tools and frameworks necessary for environmental modelling, the true test of these methods lies in their application. The transition from theory to practice involves not only technical expertise but also a deep understanding of the ecological and socio-economic contexts in which these models operate. The next section will explore several key areas where mathematical models have been successfully applied to environmental and resource management, demonstrating the practical impact of these theoretical tools.

3. Key Areas of Application

3.1 Resource Allocation Models

Mathematical models in resource allocation play a crucial role in optimizing the use of both renewable and non-renewable resources. These models help determine the most efficient and sustainable ways to distribute resources, considering various factors like economic viability, environmental impact, and social equity.

3. 1.1 Optimizing Renewable Energy Sources (Gómez Sánchez et al., 2021;  Matia et al., 2023).

Models for renewable energy optimization are vital for supporting the transition to sustainable energy systems. For instance, models can determine the optimal mix of solar, wind, hydro, and biomass energies for a given region based on factors like availability, cost, and environmental impact.

Example
A linear programming model might be used to optimize energy production and consumption in a grid. The model would include constraints related to production capacity, environmental regulations, and demand forecasts. The objective could be to minimize costs or maximize the use of renewable sources.

3.1.2 Water Resource Management (Friedman et al., 1984; Tony & Gaafar, 2017)

Water resource management models help in allocating water among various users such as agricultural, industrial, and residential sectors while ensuring sustainability. These models take into account rainfall patterns, reservoir levels, usage rates, and ecological needs.

Example: A stochastic model could be used to manage a reservoir’s water supply, taking into account unpredictable rainfall and varying demand levels. The model helps in making decisions about water release rates, storage, and conservation measures to balance human needs with ecological preservation.

3.1.3 Sustainable Agriculture (Mellaku & Sebsibe, 2022; Gharye Mirzaei et al., 2023).

In agriculture, models are used to maximize crop yields while minimizing inputs like water, fertilizers, and pesticides. These models consider soil conditions, weather data, crop genetics, and market trends to recommend planting schedules, irrigation systems, and crop rotations that optimize resource use.

Example
A simulation model could predict the outcomes of different farming techniques on crop yield and soil health, helping farmers choose practices that maintain or increase productivity without depleting resources.

3.2 Dynamics Models

Population dynamics models are fundamental tools in ecology, conservation biology, and resource management (Accolla, et al., 2021). They provide insights into how populations change over time and space, influenced by factors like birth rates, death rates, immigration, and emigration. These models are crucial for understanding species survival, community interactions, and the impact of human interventions on wildlife and ecosystems.

3.2.1 Modelling Wildlife Populations

A primary application of population dynamics models in wildlife conservation is to predict population trends and assess the risks of extinction or overpopulation (Witmer, 2005; Johnston et al., 2019). Such models help in crafting management strategies that aim to preserve endangered species or control invasive species.

Example: Logistic Growth Model (Law et al., 2003)
The logistic growth model is a classic example that describes how a population grows rapidly initially and then stabilizes as it reaches the carrying capacity of its environment. The model is given by the differential equation:

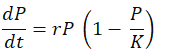
Here, (𝑡) represents the population size at time t, r is the intrinsic growth rate, and K is the carrying capacity of the environment. This model helps in understanding growth limitations and managing species under environmental constraints.

3.3 Human Demographic Models

In urban planning and public health, demographic models analyze human population trends to assist in infrastructure development, healthcare planning, and policy formulation (Grundy & Murphy, 2015). These models often incorporate factors such as age structure, fertility rates, mortality rates, and migration patterns.

Example: Leslie Matrix Model
The Leslie matrix is a discrete, age-structured model that uses matrix algebra to predict the growth and age composition of a population over time. The model is particularly useful for understanding how changes in demographic rates affect overall population dynamics.

P_t+1 ​= LP_t​
where 𝑃𝑡Pt​ is the vector representing the number of individuals in each age class at time 𝑡, and 𝐿 is the Leslie matrix, which includes survival rates and fertility rates of each age class.

3.4 Invasive Species Management

Managing invasive species is critical for preserving biodiversity and ecosystem services. Population dynamics models help in predicting the spread of invasive species and assessing the effectiveness of control measures such as culling, habitat management, and biological control (Emlen et al., 2006; Thompson et al., 2021).

Example: Reaction-Diffusion Model
Reaction-diffusion models are used to describe how invasive species spread spatially in an environment. These models combine local growth dynamics with movement across space, providing a tool for predicting how quickly and widely an invasive species might spread.

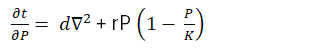
In this equation, 𝑑d represents the diffusion rate, reflecting the species’ ability to move or spread through the habitat, and ∇²𝑃 is the Laplacian, indicating spatial diffusion.

4. Case Studies of Successful Mathematical Models in Practice

4.1 Case Study 1: Managing Water Resources in California

4.1.1 Background

California faces significant water management challenges due to its variable climate and extensive agricultural needs (Pathak et al., 2018; Stewart et al., 2020). The state has employed various mathematical models to optimize water distribution, ensuring sustainability across urban, agricultural, and ecological systems.

4.1.2 Model Application

One of the key tools used is the California Simulation of Evapotranspiration of Applied Water (SIMETAW) model, which integrates weather data, soil characteristics, and crop information to predict water needs for agriculture (Orang et al., 2013).

4.1.3 Model Equation

Et_c ​= K_c ​× ET_o​
Here, 𝐸𝑇_𝑐 is the crop evapotranspiration under standard conditions, 𝐾_𝑐 ​ is the crop coefficient, and 𝐸𝑇_𝑜 is the reference evapotranspiration from nearby weather stations.

4.1.4 Outcome

This model has been crucial in making informed decisions about water allocations, particularly in drought years. It helps farmers and water managers optimize irrigation schedules and reduce water waste, contributing significantly to statewide water conservation efforts.

4.2 Case Study 2: Wildlife Conservation in the Serengeti

4.2.1 Background

The Serengeti ecosystem in Tanzania is one of the most complex environments, hosting a vast array of species, including the largest migration of land animals on earth (Estes, 2014). Mathematical models have been instrumental in managing this biodiversity hotspot (Ngana et al., 2019).

4.2.2 Model Application

The use of population dynamics models, specifically the Lotka-Volterra equations for predator-prey interactions, has been crucial in understanding the impacts of human activity and environmental changes on wildlife populations.

4.23 Model Equations

Where 𝑋 and 𝑌 represent prey and predator populations, respectively, 𝛼, 𝛽, 𝛾, and 𝛿 are parameters that describe the interaction between these species.

4.2.4 Outcome

These models help conservationists predict animal population trends and guide interventions such as anti-poaching efforts and habitat preservation. They are crucial for maintaining the ecological balance and ensuring the sustainability of both the animal populations and the local human communities depending on them.

4.3 Case Study 3: Optimizing Renewable Energy in Germany

4.3.1 Background

Germany’s Energiewende (energy transition) is one of the most ambitious national projects to shift from fossil fuels to renewable energy (Kern, 2013; Quitzow, et al., 2016). Mathematical models have played a key role in planning and implementing this transition (Savio et al., 2022).

4.3.2 Model Application

Optimization models for energy distribution have been used to manage the integration of intermittent solar and wind energy into the national grid. These models calculate the optimal storage and distribution strategies to handle variability in renewable energy production.

4.3.3 Model Equation

Minimize Z=∑ⁿ_(𝑖=1)(C_𝑖– P_𝑖)

Where 𝑍 is the total cost, 𝐶_𝑖​is the cost of energy production from source 𝑖, and 𝑃_𝑖 is the power generated from source 𝑖.

4.3.4 Outcome

The models ensure that energy supply remains stable and cost-effective, significantly contributing to achieving Germany’s goal of reducing greenhouse gas emissions while maintaining energy security.

4.4 Case Study 4: Air Quality Improvement in Beijing

4.4.1 Background

Beijing has struggled with severe air pollution due to rapid industrialization and urbanization (Li et al., 2016). Mathematical models have been central to formulating effective air quality management policies (He et al., 2023).

4.4.2 Model Application

Statistical models that incorporate weather patterns, traffic data, and industrial activity have been used to predict pollution levels and evaluate the effectiveness of various control measures.

4.4.3 Model Equation

AQI = f (PM_2.5​, PM₁₀​, CO, NO_x​, SO₂​, O₃​)

Where 𝐴𝑄𝐼 is the Air Quality Index, and the function 𝑓f integrates concentrations of particulate matter and gaseous pollutants.

4.4.4 Outcome

These models provide essential insights for policy-makers, leading to targeted interventions like traffic restrictions and industrial regulations that have significantly improved air quality in the city.

4.5 Case Study 5: Flood Risk Management in the Netherlands

4.5.1 Background

The Netherlands, a country largely below sea level, has a sophisticated approach to managing flood risks (Klijn et al., 2012; Tromp et al., 2022). Mathematical models are crucial in designing and maintaining its flood defense systems (Vrijling, 2001).

4.5.2 Model Application

Hydraulic models simulate water movement through channels, dykes, and other structures to predict flood scenarios and test the efficacy of flood defenses under various conditions.

4.5.3 Model Equation

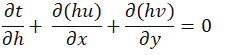
Here, ℎ is the water depth, and 𝑢 and 𝑣 are the flow velocities in the 𝑥x and 𝑦y directions, respectively.

4.5.4 Outcome

These models are pivotal in ensuring the safety and resilience of Dutch infrastructure against floods, allowing for precise planning and construction of flood barriers that protect millions of lives and significant economic assets.

4.6 Case Study 6: Agricultural Productivity and Sustainability in Ethiopia

4.6.1 Background

Ethiopia’s economy heavily depends on agriculture, which sustains the livelihoods of most of its population. However, the country faces challenges such as drought, soil degradation, and inefficient farming practices (Yigezu Wendimu, 2021). To address these issues, mathematical models have been utilized to improve agricultural productivity and sustainability.

4.6.2 Model Application

Crop simulation models are employed to optimize the use of water and fertilizers under varying climatic conditions. These models assess the impact of different farming techniques on crop yield and soil health, helping to make informed decisions that boost productivity while conserving resources.

4.6.3 Model Equation

𝑌 = 𝑓 (𝑊, 𝑁, 𝐺, 𝑇, 𝑆)    

Where 𝑌 represents the crop yield, 𝑊 is water availability, 𝑁 is nitrogen level, 𝐺 is genetic potential of the crop, 𝑇 is temperature, and 𝑆 is soil quality. This model integrates these factors to predict how changes in any of them affect crop output.

4.6.4 Outcome

The use of these models has enabled Ethiopian farmers to adapt to the variable rainfall patterns and to plan their planting and harvesting schedules more effectively. It has also guided the government and non-governmental organizations in implementing strategies such as micro-irrigation systems and soil fertility improvement programs. As a result, areas using these models have seen an increase in crop yields and a reduction in water and fertilizer wastage, significantly contributing to food security and economic stability in rural communities.

5.Challenges and Limitations of Mathematical Models in Sustainable Management

5.1 Introduction to Challenges and Limitations

While mathematical models are invaluable tools in sustainable management, they come with inherent challenges and limitations that can affect their accuracy and applicability. Understanding these challenges is crucial for effectively using models in decision-making processes and for ongoing improvements in modelling techniques.

5.2 Data Quality and Availability

One of the most significant limitations of mathematical modelling in environmental science is the quality and availability of data. Models are only as good as the data they use; inaccurate, incomplete, or outdated data can lead to misleading results.

5.2.1 Example

In developing regions, data scarcity on environmental variables such as soil moisture, rainfall, and land usage patterns can severely limit the effectiveness of models designed to predict agricultural yields or water availability. Even in developed countries, the granularity and frequency of data collection may not meet the requirements for highly detailed models.

5.3 Complexity of Natural Systems

Environmental systems are inherently complex and involve numerous interacting components, each influenced by variable factors like climate change, human activity, and ecological relationships.

5.3.1 Example

Climate models struggle to accurately predict cloud formation and its impact on climate due to the complex nature of cloud physics and the interactions with other atmospheric components. This limitation can affect the reliability of long-term weather forecasts and climate change projections.

5.4 Scaling Issues

Models are often developed for specific contexts or scales, and scaling them up or down can introduce errors. Issues arise when models designed for small-scale environments are applied to larger systems without adequate adjustment for new dynamics or when local models are generalized too broadly.

5.4.1 Example

A water management model developed for a small watershed may not be directly applicable to a larger river basin without modifications, as factors like river flow dynamics, user demands, and ecological needs can differ significantly between scales.

5.5 Uncertainty and Stochasticity

Many environmental processes are stochastic in nature, meaning they are randomly determined and thus inherently unpredictable. This randomness adds an element of uncertainty to models, which can be difficult to quantify and communicate.

5.5.1 Example

Population dynamics models for wildlife conservation must account for random events such as disease outbreaks or sudden environmental changes, which can drastically alter the outcomes predicted by deterministic models.

5.6 Model Validation and Calibration

Validating and calibrating models to ensure they reflect real-world conditions accurately is a complex and resource-intensive process. Without rigorous validation, there is a risk of relying on models that do not accurately simulate the systems they are supposed to represent.

5.6.1 Example

An air quality model must be continuously calibrated with current pollution data and meteorological information to remain accurate; failure to do so can lead to incorrect predictions that may misguide public health advisories or policy decisions.

5.7 Overreliance on Models

There is a risk of overreliance on mathematical models, especially in policy-making contexts where decisions can have far-reaching consequences. Overconfidence in models can lead to decisions that might not fully consider other important aspects like social equity, cultural values, and political contexts.

5.7.1 Example

Economic models that guide fisheries management often focus on maximizing sustainable yields but may overlook the cultural and subsistence importance of certain species to local communities, leading to conflicts and social discontent.

5.8 Ethical Considerations

The use of models in environmental management also raises ethical questions, particularly regarding who controls the model development and what biases might be inherent in the chosen methodologies.

5.8.1 Example

If a model for allocating water resources is primarily designed by agricultural interests without input from indigenous communities, it may unfairly distribute water in ways that favor large-scale farming over traditional uses.

5.9 Adaptability and Flexibility

Environmental conditions are rapidly changing due to factors like climate change and urbanization, which requires models to be adaptable and flexible. However, many models are static and cannot easily incorporate new data or reflect sudden changes in the system they represent.

5.9.1 Example

Models used for predicting urban water demand may not quickly adapt to sudden demographic changes, such as a rapid influx of residents due to migration, leading to inaccuracies in water supply planning.

6. Future Directions in Green Mathematics

6.1 Introduction to Future Trends

As the field of Green Mathematics continues to evolve, several emerging trends and technologies are shaping its future. These developments promise to enhance the accuracy, applicability, and impact of mathematical models in sustainable management. This section explores potential future directions that could significantly influence the practice of Green Mathematics.

6.2 Integration of Big Data and Machine Learning

The surge in big data technology and machine learning offers profound opportunities for enhancing mathematical models in environmental science. By integrating these technologies, models can process vast amounts of data faster and more accurately, uncovering patterns that were previously undetectable.

6.2.1 Example

Machine learning algorithms can be used to improve climate models by analysing large datasets of atmospheric conditions, allowing for more precise predictions of weather patterns and climate change impacts. These models can learn from past data to refine their predictions, adapting to new data as it becomes available.

6.3 Increased Use of Real-Time Data

Advancements in sensor technology and the Internet of Things (IoT) allow for the collection of real-time environmental data. Utilizing real-time data in mathematical models can significantly improve the timeliness and relevance of information provided for decision-making.

6.3.1 Example

Real-time water quality monitoring using IoT sensors can provide immediate data to models that predict pollution levels in rivers and lakes. This enables quicker responses to pollution incidents, potentially preventing harm to wildlife and human health.

6.4 Enhanced Model Interoperability

As the complexity of environmental issues increases, there is a growing need for models that can interact and integrate across different disciplines and scales. Enhanced interoperability among models will allow for a more holistic approach to environmental management.

6.4.1 Example

A model that integrates hydrological data with agricultural data can help in making comprehensive water management decisions that consider both the water needs of crops and the dynamics of the entire watershed.

6.5 Development of Participatory Modelling

Participatory modelling involves stakeholders in the modelling process, ensuring that various perspectives and knowledge bases are included. This approach can increase the legitimacy and acceptance of models, particularly in policy-making contexts.

6.5.1 Example

In managing a national park, a participatory model could include input from conservationists, local communities, tourism operators, and government agencies. This collaborative approach ensures that the model comprehensively addresses the needs and concerns of all stakeholders.

6.6 Advances in Predictive Uncertainty Analysis

Improving the methods used to analyse and communicate the uncertainty in model predictions is crucial for their reliability and trustworthiness. Advances in uncertainty analysis will enable better risk management and decision-making under uncertainty.

6.6.1 Example

New techniques in stochastic modelling can provide more detailed probability distributions of outcomes, such as the impact of a proposed dam on downstream ecosystems, helping decision-makers understand the range of possible scenarios and the likelihood of each.

6.7 Focus on Sustainability Metrics

Future developments in Green Mathematics should include the creation and refinement of sustainability metrics that can quantify and monitor progress towards environmental goals. These metrics are essential for assessing the effectiveness of policies and practices.

6.7.1 Example

Models that calculate carbon footprints and water footprints can help industries and governments measure their environmental impact and guide them towards more sustainable practices.

6.8 Global Collaboration and Standardization

As environmental challenges are global in nature, there is a need for increased international collaboration and standardization in modelling practices. Shared standards and models can facilitate more consistent and cooperative responses to global environmental issues.

6.8.1 Example

An international standard for modelling carbon sequestration in forests could help in aligning national efforts and pooling data for a global understanding of forestry contributions to carbon offsetting.

7. Conclusion

7.1 Summary of Key Points

This chapter has explored the significant role of Green Mathematics in promoting sustainable resource management within the broader context of environmental science. It began by establishing the theoretical foundations, setting the stage for exploring various mathematical models that address complex ecological and human challenges. Detailed case studies showcased successful implementations of these models across different regions and sectors, demonstrating their vast capabilities and impactful outcomes. The inherent limitations and challenges faced by these models were also critically examined, providing a balanced view of their current effectiveness. Looking ahead, promising future directions were identified that could enhance the scope and precision of Green Mathematics.

7.2 The Role of Mathematics in Advancing Sustainability

Mathematics serves as a powerful tool for sustainability, offering unique approaches to solving some of the most pressing environmental issues today. From optimizing resource use in agriculture and energy to managing wildlife populations and predicting climate change impacts, mathematical models bridge the gap between scientific understanding and practical environmental management. They enable policymakers, scientists, and local stakeholders to make informed decisions based on robust quantitative analyses, thereby improving the efficacy of strategies aimed at conserving our planet’s resources.

7.3 Contributions to the Book Exploring STEM Frontiers

In the context of the book Exploring STEM Frontiers, this chapter contributes to a broader dialogue about the innovative applications of science, technology, engineering, and mathematics (STEM) in tackling global challenges. Green Mathematics exemplifies how interdisciplinary approaches can yield solutions that are not only effective but also scalable and adaptable to various environmental and societal contexts. By integrating insights from mathematics with those from other scientific disciplines, the chapter underscores the synergy essential for advancing knowledge and sustainable practice.

7.4 Call to Action

As the field looks to the future, the integration of mathematical models into sustainable resource management is an ongoing journey. Continuous collaboration among mathematicians, environmental scientists, policymakers, and communities remains crucial. Enhancing the precision of these models and expanding their applicability is essential to meet the evolving demands of global sustainability challenges. Additionally, increased investment in education and research in Green Mathematics is necessary to cultivate a new generation of scientists and engineers equipped to use these tools effectively.

In conclusion, the potential of Green Mathematics to contribute to a sustainable future is immense. It is imperative to leverage this potential by addressing the current limitations of these models and exploring new methodologies that can provide deeper insights and more reliable predictions. As this field evolves, it will undoubtedly play a crucial role in shaping sustainable practices and policies worldwide, truly pushing the frontiers of STEM and paving the way for a more resilient and sustainable planet.

Conflict of Interest

The research was completed with no conflict of interest.

References

Accolla, C., Vaugeois, M., Grimm, V., Moore, A. P., Rueda‐Cediel, P., Schmolke, A., & Forbes, V. E. (2021). A review of key features and their implementation in unstructured, structured, and agent‐based population models for ecological risk assessment. Integrated environmental assessment and management, 17(3), 521-540. https://doi.org/10.1002/ieam.4362

Barwell, R. (2018). Some Thoughts on a Mathematics Education for Environmental Sustainability. In: Ernest, P. (eds) The Philosophy of Mathematics Education Today. ICME-13 Monographs. Springer, Cham. 145-160. https://doi.org/10.1007/978-3-319-77760-3_9

Billionnet, A. (2013). Mathematical optimization ideas for biodiversity conservation. European Journal of Operational Research, 231(3), 514-534. https://doi.org/10.1016/j.ejor.2013.03.025

Emlen, J. M., Duda, J. J., Kirchhoff, M. D., & Freeman, D. C. (2006). Interaction assessment: a modelling tool for predicting population dynamics from field data. Ecological modelling, 192(3-4), 557-570. https://doi.org/10.1016/j.ecolmodel.2005.07.012

Estes, R. D. (2014). The Gnu’s world: Serengeti wildebeest ecology and life history. University of California Press.

Filipsson, M. (2011). Uncertainty, variability and environmental risk analysis (Doctoral dissertation, Linnaeus University Press). https://www.diva-portal.org/smash/get/diva2:405602/FULLTEXT01.pdf

Friedman R., Ansell C., Diamond S., & Haimes Y. Y. (1984). Use of models for water resources management, planning, and policy. Water Resource Research. 20 (7). 793-803.  https://doi.org/10.1029/WR020i007p007 93

Gharye Mirzaei, M., Gholami, S., & Rahmani, D. (2023). A mathematical model for the optimization of agricultural supply chain under uncertain environmental and financial conditions: the case study of fresh date fruit. Environment, Development and Sustainability, 1-34. https://doi.org/10.1007/s10668-023-03503-7

Gómez Sánchez, M., Macia, Y. M., Fernández Gil, A., Castro, C., Nuñez González, S. M., & Pedrera Yanes, J. (2021). A mathematical model for the optimization of renewable energy systems. Mathematics, 9(1), 39. https://doi.org/10.3390/math9010039

Grundy, E., & Murphy, M. J. (2015). Demography and public health. ‘Demography and public health’, in Roger Detels et al., (Eds), Oxford Textbook of Global Public Health, 6 edn, https://doi.org/10.1093/med/ 9780199661756.003.0126

He, S., Tang, S., Zhang, Q., Rong, L., & Cheke, R. A. (2023). Modelling optimal control of air pollution to reduce respiratory diseases. Applied Mathematics and Computation, 458, 128223. https://doi.org/10.1016/ j.amc.2023.128223

IBM (2024).What is optimization modelling?IBM. Retrieved from https://www.ibm.com/topics/optimization-model Accessed May 2, 2024

Johnston, A. S., Boyd, R. J., Watson, J. W., Paul, A., Evans, L. C., Gardner, E. L., & Boult, V. L. (2019). Predicting population responses to environmental change from individual-level mechanisms: towards a standardized mechanistic approach. Proceedings of the Royal Society B, 286(1913), 20191916.

Kern, F. (2013). Implementing the green economy. Ökologisches Wirtschaften-Fachzeitschrift, 28(3), 20-22.

Klijn, F., de Bruijn, K. M., Knoop, J., & Kwadijk, J. (2012). Assessment of the Netherlands’ flood risk management policy under global change. Ambio, 41, 180-192. https://doi.org/10.1007%2Fs13280-011-0193-x

Kundu, S. (2018). Mathematical modelling as a tool for sustainable development. J. Artic. Math. Educ, 5, 348-350. http://ijrar.com/upload _issue/ijrar_issue_1052.pdf

Law, R., Murrell, D. J., & Dieckmann, U. (2003). Population growth in space and time: spatial logistic equations. Ecology, 84(1), 252-262. https://doi.org/10.1890/0012-9658(2003)084[0252:PGISAT]2.0.CO;2

Li, X., Song, J., Lin, T., Dixon, J., Zhang, G., & Ye, H. (2016). Urbanization and health in China, thinking at the national, local and individual levels. Environmental Health, 15, 113-123. https://doi.org/10.1186/s 12940-016-0104-5

Li, Y. P., Huang, G. H., Nie, S. L., Chen, B., & Qin, X. S. (2013). Mathematical modelling for resources and environmental systems. Mathematical Problems in Engineering, 2013.

Liu, J., Li, Y. P., & Huang, G. H. (2013). Mathematical modelling for water quality management under interval and fuzzy uncertainties. Journal of Applied Mathematics, 2013. https://doi.org/10.1155/2013/731568

Matia, S. N., Mahata, A., Paul, S., Mukherjee, S., Alam, S., & Roy, B. (2023). A study on imprecise mathematical model for optimal management and utilization of renewable resource by population. Results in Control and Optimization, 12, 100252. https://doi.org/10.1016/j.rico.2023 .100252

Mbagwu, J. P., Obidike, B. M., Chidiebere, C. W., & Enyoh, C. E. (2021). Series Solutions of Mathematical Modelling of Environmental Problems. World Scientific News, 160, 91-110.

Mellaku, M. T., & Sebsibe, A. S. (2022). Potential of mathematical model-based decision making to promote sustainable performance of agriculture in developing countries: A review article. Heliyon, 8(2). https://doi.org/10.1016/j.heliyon.2022.e08968

 Ngana J. J. , Luboobi L.S., Abonyo O. J. (2019). Mathematical Model for the Serengeti Ecosystem under Weather Variations, American Journal of Computational and Applied Mathematics, 9(3), 85-95. doi: 10.5923/j.ajcam.20190903.04.

Orang, M. N., Snyder, R. L., Shu, G., Hart, Q. J., Sarreshteh, S., Falk, M., … & Eching, S. (2013). California simulation of evapotranspiration of applied water and agricultural energy use in California. Journal of Integrative Agriculture, 12(8), 1371-1388. https://doi.org/10.1016/S2095-3119(13)60742-X

Pathak, T. B., Maskey, M. L., Dahlberg, J. A., Kearns, F., Bali, K. M., & Zaccaria, D. (2018). Climate change trends and impacts on California agriculture: a detailed review. Agronomy, 8(3), 25. https://doi.org/ 10.3390/agronomy8030025

Pianosi, F. (2014). Computational models for environmental systems. In Amigoni F. & Schiaffonati V. (Eds.). Methods and Experimental Techniques in Computer Engineering. SpringerBriefs in Applied Sciences and Technology, 3-13. http://dx.doi.org/10.1007/978-3-319-00272-9_1

Quitzow, L., Canzler, W., Grundmann, P., Leibenath, M., Moss, T., & Rave, T. (2016). The German Energiewende–What’s happening? Introducing the special issue. Utilities Policy, 41, 163-171. https://doi.org/10. 1016/j.jup.2016.03.002

Rehmeyer, J., Cozzens, M., & Roberts, F. S. (2011). Mathematical and statistical challenges for sustainability. Providence: RI American Mathematical Society.

Savio, A., De Giovanni, L., & Guidolin, M. (2022). Modelling energy transition in Germany: An analysis through ordinary differential equations and system dynamics. Forecasting, 4(2), 438-455. https://d oi.org/10.3390/forecast4020025

Stewart, I. T., Rogers, J., & Graham, A. (2020). Water security under severe drought and climate change: Disparate impacts of the recent severe drought on environmental flows and water supplies in Central California. Journal of Hydrology X, 7, 100054. https://doi.org/10.1016/j. hydroa.2020.100054

Thompson, B. K., Olden, J. D., & Converse, S. J. (2021). Mechanistic invasive species management models and their application in conservation. Conservation Science and Practice, 3(11), e533. https://doi.org/10.1111/csp2.533

Tony, M. S. S., & Gaafar, I. (2017). Applying Mathematical Models in Water Management and Irrigation Projects.

Tromp, E., te Nijenhuis, A., & Knoeff, H. (2022). The Dutch flood protection programme: Taking innovations to the next level. Water, 14(9), 1460. https://doi.org/10.3390/w14091460

Vrijling, J. K. (2001). Probabilistic design of water defense systems in The Netherlands. Reliability engineering & system safety, 74(3), 337-344. https://doi.org/10.1016/S0951-8320(01)00082-5

Witmer, G. W. (2005). Wildlife population monitoring: some practical considerations. Wildlife Research, 32(3), 259-263. https://doi.org/10.1 071/WR04003

Yigezu Wendimu, G. (2021). The challenges and prospects of Ethiopian agriculture. Cogent Food & Agriculture, 7(1), 1923619. https://doi.org/ 10.1080/23311932.2021.1923619

Zeidan, B. A. (2017). Mathematical modelling of environmental problems. In Seiichiro Y.  Bhola R. G., & J.N. Govil (Eds.) Environmental Science and Engineering, Instrument, Modelling and Analysis, 7. Studium Press LLC, USA. 422-461.

Zhao, S., Qi, Z., & Lu, J. (2024). The role of differential equations in environmental science modelling. International Journal of Mathematics and Systems Science, 7(2).

About this Article

Cite this Article

APA

Akinsemolu A. A. (2024). Green Mathematics: Harnessing Mathematical Models for Sustainable Resource Management. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.

Chicago

Adenike A. Akinsemolu . 2024. “Green Mathematics: Harnessing Mathematical Models for Sustainable Resource Management.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.

Corresponding Author Email: famuagunks@aceondo.edu.ng

Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.

Distributed under Creative Commons CC-BY 4.0

Share this article

Use the buttons below to share the article on desired platforms.