Relating the Volumes of Rectangular and Conical Frustums

Olagunju S. O.¹

¹Adeyemi Federal University of Education, Ondo State, Nigeria

*Corresponding Author Email: lagsam2016@gmail.com …

Read More

Highlights

Abstract

The utility of diverse forms of knowledge is paramount for the development of any society and the continuation of its advancements. It is observed that children show increased interest in types of knowledge that they find to be applicable and relatable to their experiences. Building on an earlier presentation that discussed the volumes of various frustums, this paper delves into exploring the relationship between the volumes of Conic and Rectangular Frustums. Moreover, it demonstrates that it is feasible to estimate the volume of one frustum type based on the known volume of the other, provided certain conditions, as outlined by Olagunju (2011), are satisfied. This is accomplished through the application of validated formulas for calculating the volumes of Conical and Rectangular Frustums, V_CF=1/12 πh (D²+Dd+d²) and V_RF=h/∛5 (D²+Dd+d²) respectively, which were found to be related.

Keywords: Volume, Pyramids, Frustum, Rectangular, Conical, Diagonals.

1. Background

Progressive scientific knowledge necessitates advancements in application to foster continuous development. This is particularly true for mathematics education, where there is a constant need to refine and improve upon existing problem-solving methods. This necessity is the driving force behind revisiting proven formulas for calculating the volumes of Rectangular-based and Circular-based Frustums and devising a formula to bridge the two. 

2. Significance of the Study

This linkage aims to enable the use of the volume of one type of frustum to estimate the volume of the other, thereby streamlining estimations for scholars and other stakeholders.

3. Classification of Pyramids and Frustums

Olagunju (2011) characterizes Pyramids as polyhedrons with one polygonal face known as the ‘base’ and all other faces as triangles converging at a point referred to as the ‘apex’. A Cone or a Conical Pyramid is identified as a special kind of pyramid whose base is circular, and all slant edges converge at the vertex. When a section of a Pyramid is sliced away from the apex, it results in a Truncated Pyramid, commonly termed a Frustum. Pyramids are categorized by their dimensions, with a Regular Pyramid having a base that is a regular polygon (e.g., Square-Based, Rectangular-Based) and a Right Pyramid being one where the apex is connected to the center of the base by a perpendicular line. An Arbitrary Pyramid is described as having a singular cross-sectional shape with lengths that scale linearly with its height.

4. Brief Information on Volumes of Conical and Rectangular Frustums

Olagunju (2011, 2016), drawing upon the work of Harris and Stocker (1998), demonstrated that the volume of a pyramid is calculated as one-third of the product of the base area and the perpendicular height. This can be succinctly expressed as:

That is Pyramidal Volume = 1/3(base-area x height)

Thus, the volume of the Truncated Pyramid (i.e. Pyramidal Frustum) is given as the difference between the complete pyramid and the chopped small pyramid.

That is V_PF= V_BP-V_SP

Where V_PF= Volume of the Pyramidal Frustum,
V_BP= Volume of the complete Big Pyramid
V_SP = Volume of the small chopped pyramid

4.1.1 Volume of a Conical Frustum

Consider the Conical Frustum above. Macrae et’al (2001) led us through the method used to obtain the volume of a Conical Frustum (or simply ‘a cone’) popularly referred to Hero’s formula,  here designated as V_CF is given as V_CF=1/3 πh (R²+Rr+r²)

Where V_CF= Volume  of Square-based Frustum, 
R  = Radius of the large Circular base,
r   = Radius of the small Circular top, 
and h  =  the height of the Conical Frustum.

But Olagunju (2011) considered the said hero’s formula thus:

As usual, let D = Diameter of circular base, d = Diameter of circular top,

Applying the usual fact that R=1/2 D and r=1/2 d

Then, Conical Frustum Volume = 1/3 πh ((D/2)²+D/2+d/2+ (d/2)²)

=1/3 πh (D²/4+Dd/4+(d²/4)

=1/41/3 πh ((D²+Dd+d²)

Hence, Conical Frustum Volume V_CF=1/12 πh (D²+Dd+d²) (4.1)

4.1.2 Volume of a Rectangular Frustum

Therefore, the volume of a Truncated Pyramid, also known as a Pyramidal Frustum, is determined by subtracting the volume of the smaller, removed pyramid from the volume of the complete pyramid.

In further detail, considering a Rectangular Frustum, Olagunju (2017) applied the standard procedure of calculating the volumes of the larger and smaller pyramids. By subtracting the volume of the smaller pyramid from the larger one, he derived a tested and proven formula for the volume of a rectangular frustum. This formula takes into account:

Base-Length = 2L, Base-breadth = L, Top-Length = 2l, Top-breadth = l

And that x = height of Small Pyramid, h = height of Frustum,

Where  H = Height of Large Pyramid, (height of small pyramid + height of Frustum)

If the base and top diagonals of the pyramidal frustum be D and d respectively.

Since its height is  h,  and the Volume is designated as  ,

Then, by the old method, the Volume of Rectangular Frustum will be the difference between the

Volume of large Rectangular Pyramid and Volume of chopped Rectangular Pyramid. Thus,  

    Considering similarity of ∆s if the pyramids are completed, we have

   So, the volume of a Rectangular Frustum is V_RF=2h/15πh (D²+Dd+d²) (4.2)

5. Relationship between Volumes of Conical and Rectangular Frustums

5.1 Lemma

The Rectangular Frustum must have the Diagonals of the base and top rectangles to be equal to the Diameters of the respective base and top circles of the Conical Frustum. (1.1)

The height of the Rectangular Frustum must be equal to the height of the Conical Frustum. (1.2)

5.3 Relationship between Volumes of Rectangular and Conical Frustums

From equations (4.1) and (4.2) above,

The Volume of the Conical Frustum V_CF=1/12 πh (D²+Dd+d²) (4.1)

And Volume of the Rectangular Frustum V_RF=2h/15πh (D²+Dd+d²) (4.2)

By Lemmas 1.1,

Height of Rectangular Frustum = Height of Conical Frustum

Also by Lemma 1.2,

Diagonal of the Top small Rectangle = Diameter of the Top small Circle and Diagonal of the Base big Rectangle = Diameter of the Base big Circle

Thus, relating equations (4.1) and (4.2), we have

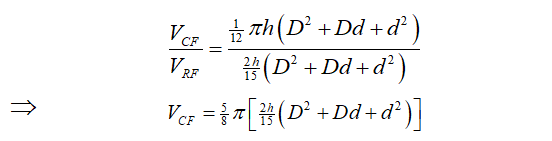
V_CF=5/8 π [Rectanguar Frustum’s Volume] (5.1)

Equation (5.1) therefore shows that the Volume of a Conical Frustum equals the product of 5π and Rectangular Frustum’s Volume divided by 8

5.3.1 Summary

From the foregoing, we arrived at the facts that:

The Volume of the Conical Frustum V_CF=1/12 πh (D²+Dd+d²) (4.1)

The Volume of the Rectangular Frustum V_RF=2h/15πh (D²+Dd+d²) (4.2)

Relating (4.1) and (4.2), we obtained   V_CF=5π/8 [2h/15 (D²+Dd+d²) ]

V_CF=5/8 π [Rectangular Frustum’s Volume] (5.1)

We illustrate as follows, using the Diagonals (Diameters) only, irrespective of the lengths and radii.

5.3.2 Illustration I

Suppose that h=5, d=4 and D=8 ,

Then, we have from (4.1),

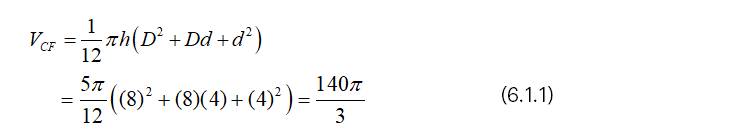
And we have from (4.2),

From (6.1.3), it is clear that V_CF=5π/8 (V_RF)

Hence, equation (5.1) holds.

5.3.3 Illustration II

Suppose that h=7, d=11 and D=22,

Then, we have from (4.1),

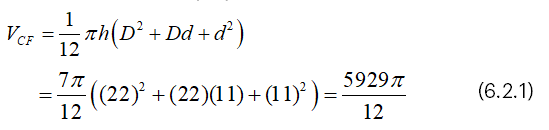
And we have from (4.2),

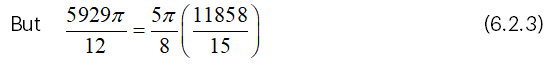
From (6.2.3), it is clear that V_CF=5π/8 (V_RF) .

Hence, equation (5.1) holds

5.3.4 Illustration III

Suppose that h=0.8, d=0.3 and D=0.6,

Then, we have from (4.1),

And we have from (4.2),

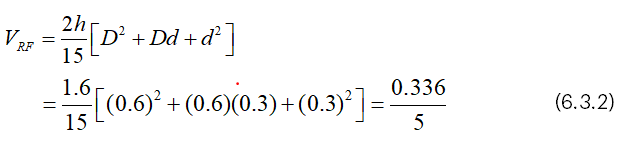
From (6.3.3), it is clear that V_CF=5π/8 (V_RF) .

Hence, equation (5.1) holds.

5.3.5 Illustration IV

Suppose that h=14, d=4 and D=12,

Then, we have from (4.1),

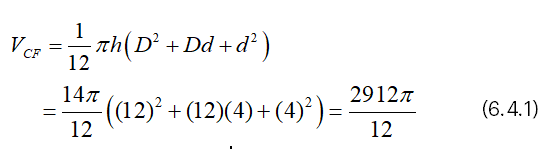
And we have from (4.2),

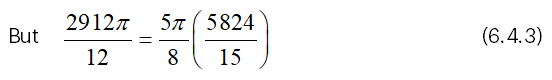
From (6.4.3), it is clear that V_CF=5π/8 (V_RF) .

Hence, equation (5.1) holds.

5.3.6 Illustration V

Suppose that h=2.7, d=0.6 and D=2.4,

Then, we have from (4.1),

And we have from (4.2),

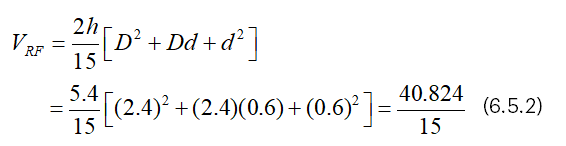
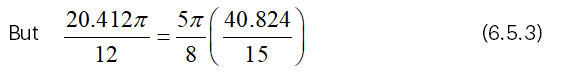
From (6.5.3), it is clear that V_CF=5π/8 (V_RF).

Hence, equation (5.1) holds

5.3.7 Illustration VI

Suppose that h=10.2, d=3.0 and D=7.5,

Then, we have from (4.1),

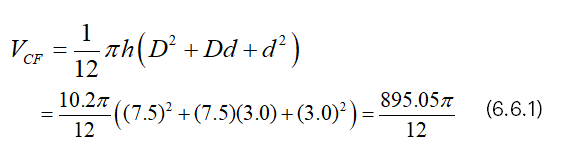
And we have from (4.2),

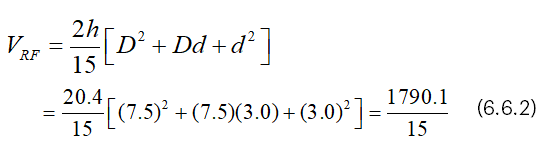
From (6.6.3), it is clear that V_CF=5π/8 (V_RF).

Hence, equation (5.1) holds.

6. Precaution

However, it is critical to highlight that each model or formula comes with its own set of caveats. The accuracy of this method is contingent upon the strict adherence to the stated conditions and the correct application of the formulas. Deviations from these prerequisites might result in discrepancies between the estimated and actual volumes, thus not achieving the anticipated precision.

7. Recommendation

Given this established connection, it is advised that students and institutions looking to calculate the volume of a Conical Frustum can now do so more conveniently by referring to the volume of a Rectangular Frustum, assuming the latter is already known. This method offers a practical approach to volume estimation, enhancing educational tools and practical applications in fields requiring geometric computations. Nonetheless, the importance of precision in applying the conditions and formulas cannot be overstressed, ensuring the reliability and accuracy of the volume estimations derived from this method.

6.Conclusion

Following the discussions and formulae presented, a significant linkage has been formed between the volume of a Conical Frustum and that of a Rectangular Frustum. This relationship suggests that the volume of a Conical Frustum can be approximated using the known volume of a Rectangular Frustum. Hence, the volume of one frustum type can serve as a basis for estimating the volume of the other, on the condition that the Top and Base Diagonals of the Rectangular Frustum are equivalent to the Top and Base Diameters of the Conical Frustum in question.

Conflict of Interest

The research was completed with no conflict of interest.

References

Harris, J. W., & Stocker, H. (1998). Pyramid. In Handbook of mathematics and computational science (pp. 98-99). Springer-Verlag.

Macrae, M. F., Kalejaye, A. O., Chima, Z. I., Garba, G. U., Ademosu, M., Chanon, J. B., Smith, A. M., & Head, H. C. (2001). New general mathematics for senior secondary schools Bk I (3rd ed., pp. 160–173). Pearson Education Limited.

Olagunju, S. O. (2011). Volume of a square-based frustum: Alternative formula (Lagsamolu Equation). In I. Nwakpa & A. Akinbile (Eds.), Meeting the challenges in science education (pp. 81–93). Babson Press.

Olagunju, S. O. (2016). The possibility of estimating the volume of a square frustum using the known volume of a conical frustum. In INCEDI (Ed.), Education delivery and new learning technologies (pp. 93–102). Methodist University College, Ghana. Retrieved from www.incedi.org

Olagunju, S. O. (2017). Estimating the Volume of a Rectangular Frustum through Relationship with a Conical Frustum (Unpublished).

About this Article

Cite this Article

APA

Olagunju S. O. (2024). Relating the Volumes of Rectangular and Conical Frustums. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.

Chicago

Olagunju S. O. 2024. “Relating the Volumes of Rectangular and Conical Frustums.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.

Corresponding Author Email: famuagunks@aceondo.edu.ng

Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.

Distributed under Creative Commons CC-BY 4.0

Share this article

Use the buttons below to share the article on desired platforms.