Application of GKSL Master Equation of Infinitesimal Generator of Decoherence-free Subalgebra of Uniformly Continuous Quantum Markov Semigroup

E. A. Oluwafemi;¹ , M. O. Ogundiran;² , I. O. Adisa;³ & J. I. Opadara.³

¹Adeyemi Federal University of Education, Ondo State, Nigeria

*Corresponding Author Email: oluwafemiabiodun1234@gmail.com …

Read More

Highlights

Abstract

In this work, we develop an analog of Gorini-Kossakowski-Sudarshan-Lindblad(GKSL) for the infinitesimal generator of decoherence-free subalgebra of Quantum Markov semigroup. The GKSL developed was then applied on M_n(c). The result showed that the matrix space M_n(c) = V₀ ⊕ V₋ will not decohere under N(T), i.e V₀ = N(T) implies M_n(c) = N(T) since V− = {0}. Also by introducing GKSL of N(T) on M_n(c), L(x ^∗x) = 0.

Keywords: Decoherence-free subalgebra, Infinitesimal generator, quantum Markov semigroup, eigenvalue and eigenvector.

1. Introduction

A subspace of a quantum system Hilbert space that is invariant to non-unitary dynamics is called a decoherence-free subspace(DFs). The subject of quantum information processing (QIP) began the study of decoherence-free subspace with a search for structured methods to avoid decoherence. Identification of particular states which have the potential of being unchanged by certain decohering processes ( i.e certain interaction with the environment )was included as one of the methods. These studies started with observations made by Pazy, 1983 who studied the consequences of pure dephasing on two qubits that have the same interaction with the environment. They found that two such qubits do not decohere. They also characterized decoherence- free subspace (DFs) as a special class of quantum error correcting codes.

In the approach of Blanchard and Olkiewicz, 2006, if the space is an algebraic space (i.e a von Neumann or a C*-algebra), the decoherence- free subspace becomes a decoherence-free subalgebra. Therefore, if a von Neumann algebra is a quantum system (say open), there is a part of the algebra that behaves like a closed system (i.e a part that is decoherence-free). This can be used to study the asymptotic behaviour of the quantum system.The evolution of a closed quantum system which does not interact with the environment, can be described by a one-parameter group of automorphism (at)t≥0 , with at(x) = e itHxe−itH and H self-adjoint. Inside an open Quantum system, sometimes, one can have a subsystem evolving like a closed quantum system where the typical effects of the interaction with the environment do not appear and the typical quantum features of the system, like quantum coherence and entanglement of quantum states are preserved (Dhari et al., 2010). Some years ago, alots of people have been showing interest in the use of Quantum Markov Semigroup to model open quantum systems having subsystems which are not affected by decoherence. In these applications, the Quantum Markov Semigroup (in the Heisenberg picture) acts as a semigroup of automorphisms of a von Neumann subalgebra N(T) of B(h), called the Decoherence-free subalgebra. This subalgebra allows identification of noise protected subsystems where states evolve unitarily, moreover its structure and relationship with the set of fixed points also has important consequences on the asymptotic behavior of the Quantum Markov Semigroup. Decoherence-free subalgebra allows us to gain insight into the structure of a Quantum Markov Semigroup, its invariant states and environment induced decoherence. Indeed, its structure as a von Neumann algebra has important consequences on the structure and the action of the whole Quantum Markov Semigroup (Fagnola& Rebolledo, 2008).

This paper focuses on the application of Gorini-Kossakowski-Sudarshan-Lindblad(GKSL) master equation of infinitesimal generator of decoherence-free subalgebra of uniformly continuous Quantum Markov semigroup.The GKSL was applied on the matrix space Mn(c) = V0 ⊕ V−. The behaviours of the matrix space under Decoherence-free Subalgebra of Quantum Markov Semigroup and GKSL master equation were the major concern of this paper.

2. The Decoherence-free Subalgebra of a Quantum Markov Semigroup(QMS)

Suppose h is a complex separable Hilbert space. A QMS B(h) is a semigroup T = (Tt)t≥0 of completely positive, identity preserving normal maps which is also weakly-∗-continuous. If T is uniformly continuous, namely norm continuous, its generator L can be represented in the well-known (Ogundiran, 2015; Sinha & Goswami, 2007) Gorini-KossakowskiSudarshan-Lindblad (GKSL) form as

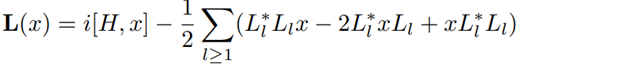
where H=H* and (L)_l≥1are operators on h such that the series ∑_l≥1L_i*L₁ is strongly convergent and [.,.] denotes the commutator [x,y]=xy-yx. The decoherence-free (DF) subalgebra of T is defined by;

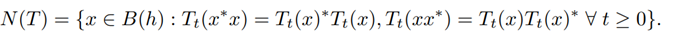
It is a well-known fact that N(T) is the biggest von Neumann subalgebra of B(h) on which every Tt acts as a ∗-endomorphism (Evans,1977).

2.1 Preliminaries

The following definitions, lemmas and propositions are necessary for our results

Definition 1 (Bratelli et al., 1987): A normed vector space is vector space (V, F) associated with a function ,∥.∥:v→R, called a norm. that obeys the following axioms

(1)  ∀ u∈V,∥u∥≥0
(2)  ∀ v∈V,∀α∈F,∥αv∥=|α|∥v∥
(3)  ∀ v,u∈V,∥u+v∥≤∥u∥+∥v∥

Definition 2 (Bratelli et al., 1987): Let V be a vector space. An inner product on V is a rule that assigns to each pair v,w ∈ V a real number ⟨v, w⟩ such that, for all u,v,w, ∈ V and α ∈ R ,

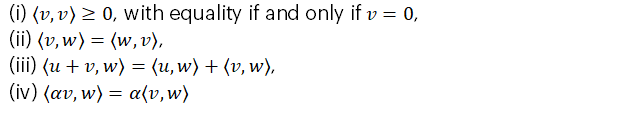
Definition 3 (Bratelli et al., 1987): Suppose X be a nonempty set. A function P: X × X → R is known as a metric provided for all x, y, and z in X,

(1) P(x, y) > 0,
(2) P(x, y) = 0 if and only if x = y,
(3) P(x, y) = P(y, x),
(4) P(x, y) ≤ P(x, z) + P(z, y)

A metric space is made up of a nonempty set and a metric on the set.

Definition 4 (Bratelli et al., 1987): Let A be an n × n matrix and let X ∈ C n be a nonzero vector for which AX = λX for some scalar λ. Then λ is called an eigenvalue of the matrix A and X is called an eigenvector of A associated with λ, or a X-eigenvector of A.

Definition 5 (Parthasarathy, 1992): The infinitesimal generator of the Quantum Markov semigroup {Tt, t ≥ 0} is a linear ( but not necessarily bounded) operator L : D(L) → A

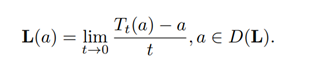
Where D(L) is the domain of L.

Definition 6 (Bratelli et al., 1987): Suppose U is a vector space over a field C, U is called an algebra if it is equipped with a multiplication law which associates to each pair A, B ∈ U, the product A · B and for every A, B, C ∈ U, the following properties are satisfied

(1) A.(B.C) = (A.B).C (associativity),
(2) A.(B + C) = A.B + A.C (distributive); and
(3) αβ(A.B) = (αA).(βB); α, β ∈ C.

Definition 7 (Bratelli et al., 1987): A subspace B of U which is also an algebra with respect to the operations of U is called a subalgebra.

Definition 8 (Bratelli et al., 1987): A mapping A ∈ U → A∗ ∈ U is called an involution or adjoint operation of the algebra U if it has the following properties:

(1) A∗∗ = A,
(2) (AB) ∗ = B∗A∗ ; and
(3) (αA + βB) ∗ = αA∗ + βB∗,
where α, β are complex conjugates of α and β respectively.

Definition 9 (Bratelli et al., 1987): An algebra with an involution is called a ∗-algebra.

Definition 10 (Parthasarathy, 1992): A von Neumann algebra on H is a ∗ -subalgebra A of L^∞(H) such that A = A^II .

Definition 11(Accardi et al., 1999): A quantum dynamical semigroup (QDS) on Von Neumann algebra A is a family of bounded linear maps {Tt, t ≥ 0} on A that satisfies the following conditions:

(1) T₀(a) = a, for all a ∈ A;
(2) T_t+s(a) = Tt(Ts(a)) = Ts(Tt(a)), for all s, t ≥ 0 and all a ∈ A;
(3) Tt is completely positive for all t ≥ 0;
(4) Tt is a normal operator on A for all t ≥ 0, that is, for every increasing net (aα)α in A with Tt(vαaα) = vαTt(aα) whenever vαaα ∈ A; or equivalently, Tt is a σ-weakly continuous operator in A for all t ≥ 0. That is, the map a → tr(ρTt(a)) is continuous from A to C for each ρ ∈ S(A), where S(A) is a set of quantum state on A.

Definition 12 (Agredo, 2014): A quantum dynamical semigroup {Tt, t ≥ 0} on A is said to be a quantum Markov (respectively, sub-Markov) semigroup if
Tt(I) = I, (respectively, Tt(I) ≤ I) ∀ t ≥ 0

3. Main Results

Here, we develop an analog of (GKSL) for the infinitesimal generator of decoherence-free subalgebra of Quantum Markov semigroup.

Definition 13: The infinitesimal generator of the Quantum Markov semigroup {Tt, t ≥ 0} on a decoherence-free subalgebra will be defined as a linear (but not necessarily bounded) operator L:D(L) → N(T) such that

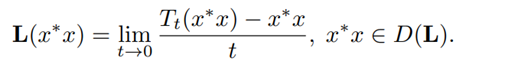
The domain of L, denoted by D(L), is the collection of x ∗x ∈ N(T) such that the above limit exists.

3.0.1 Theorem:

The GKSL equation

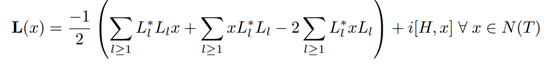
in terms of the decoherence-free subalgebra of a Quantum Markov semigroup is

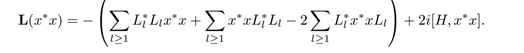
3.0.2 Proof:

Suppose the infinitesimal generator of a Quantum Markov semigroup on X is

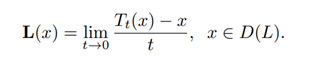
where the domain of L, denoted by D(L), is the collection of x ∈ X for which the limit exists.

Let x ∈ N(T). Then

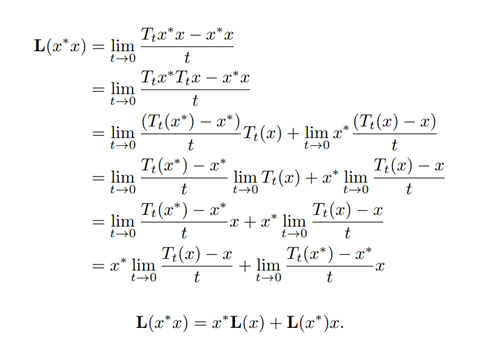
The GKSL form of L is

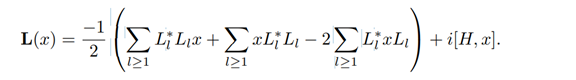
Substituting the GKSL equation in (1), we have

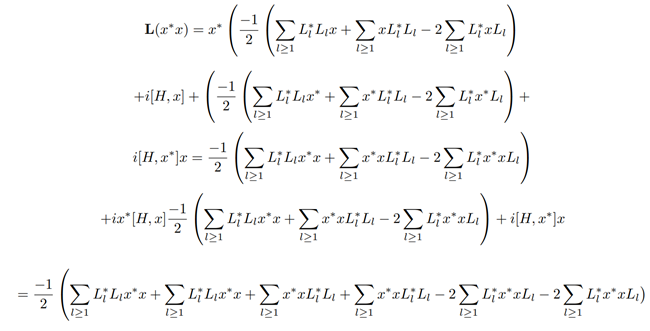
Hence, the GKSL equation in terms of the decoherence-free subalgebra of a Quantum Markov semigroup is

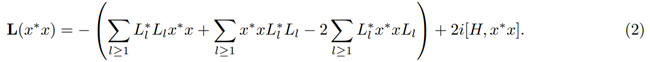
Example 1: Let

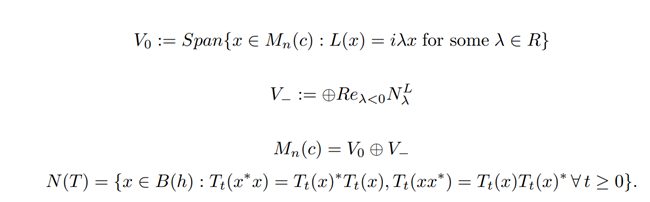
Consider a QMS T generated by L(x) = i[H, x]. Then we have V0 = N(T) = Mn(c), simply because the semigroup is

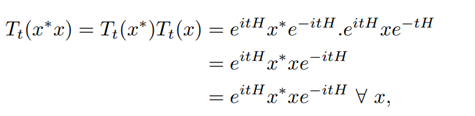
so N(T) = Mn(c), V− = {0} and consequently V0 = N(T).

Example 2:

Let u, v in c n be two linearly independent vectors where k u k=k v k= 1. Introducing a generator L on Mn(c) by

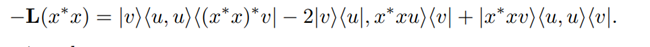
Since ⟨u,u⟩ =1 we have

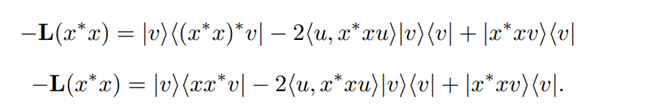
This is the generator of a QMS since it can be written in the lindblad form with H = 0 and =L₁= |u⟩⟨v|, L₁ for l ≥2 . Moreover, we have N(T) = {L, L∗} 0 ⊆ Ker(L) ⊆ V₀.We want to prove that, in some cases, V₀ is strictly bigger than N(T) and is not always an algebra. We characterize V0, Kerl and N(T) and determine the invariant states for these generators. In order to do this, it will be useful to know the spectrum of L. So consider an eigenvalue λ of the generator and notice that

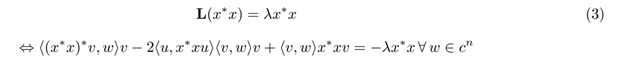
w⊥v, we have

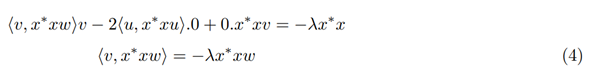
For w=v, we have

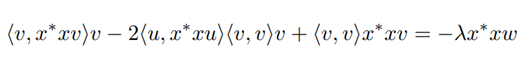
since 〈v,v〉=‖v‖²=1 we have

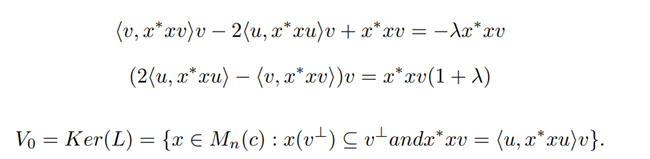
When λ = 0, (3) and (4) give

and

Then ker(L) is the space described before. In order to see that it coincides with V0, we can always use (6) and (7) for a purely imaginary λ and we easily conclude that L cannot have a non-null eigenvalues with null real part.

4. Conclusion

The result showed that the matrix space M_n(c)=V₀⊕V₋ will not decohere under N(T), i.e V₀ = N(T) implies M_n(c) = N(T) since V− = {0}. Also by introducing GKSL of N(T) on M_n(c),L(_{x^* x})=0.

Conflict of Interest

There is no conflict of interest during the completion of the research. 

---

References

Accardi L. and Kozyrev V., On the structure of quantum Markov flows, preprint Centro V. Volterra 1999.

Agredo F., Fagnola F. and R. Rebolledo (2014), Decoherence free subspaces of a quantum Markov semigroup, J. Math. Phys. 4 1343-1362

Blanchard, P. and Olkiewicz, R. (2006). Decoherence as irreversible dynamical process in open quantum systems. Open quantum systems, Recent developments Vol. III, Springer-Verlag Berlin, 117-159.

Bratelli, O. and Robinson, D. W. (1987). Operator Algebras and Quantum Statistical Mechanics, Vol. 1, Springer-Verlag, 2nd edition.

Dhari, A., Fagnola F. and Rebolledo, R. (2010). infin, Dimens. Anal. Quantum Probab. Relat. Top. 13 , 413.

Evans D. E. (1977). Commun. Math. Phys. 54, 293.

Fagnola, F. and Rebolledo, R. (2006). Notes on the Qualitative Behaviour of Quantum Markov Semigroups Open quantum systems, Recent developments. Vol. III, Spinger Berlin, 161-205.

Fagnola, F. and Rebolledo, R. (2008). Infin. Dimens. Anal. Quantum Probab. Relat. Top. 11, 467.

Ogundiran M. O., (2015). On the mild solutions of Quantum stochastic evolution inclusions, Communications in Appl. Anal., 19(2015),2,307-318.

Parthasarathy K. R. (1992). An introduction to Quantum stochastic calculus, Monographs in Mathematics Vol. 85, Birkhauser-Verlag, Basel-Boston-Berlin, 1992.

Pazy, P. (1983). Semigroups of linear operators and applications to partial differential equation. SpringerVerlag New York, inc.

Sinha K. B. and Goswam D. (2007). Quantum Stochastic Processes and Non-Commutative Geometry, Cambridge University Press.

About this Article

Cite this Article

APA
E. A. Oluwafemi, M. O. Ogundiran, I. O. Adisa;  & J. I. Opadara (2024).Application of GKSL Master Equation of Infinitesimal Generator of Decoherence-free Subalgebra of Uniformly Continuous Quantum Markov Semigroup. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.

Chicago

E. A. Oluwafemi, M. O. Ogundiran, I. O. Adisa & J. I. Opadara 2024. “Application of GKSL Master Equation of Infinitesimal Generator of Decoherence-free Subalgebra of Uniformly Continuous Quantum Markov Semigroup.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.

Corresponding Author Email: isabellanyambayo@gmail.com

Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.

Distributed under Creative Commons CC-BY 4.0

Share this article

Use the buttons below to share the article on desired platforms.