On Drift-Implicit and Full-Implicit Euler-Maruyama Methods for Solution of First Order Stochastic Differential Equations

Ganiyu A. A.;¹ , Kayode S. J.;² , Augustine A. C.;² & & Fakunle I.³

¹Adeyemi Federal University of Education, Ondo State, Nigeria

*Corresponding Author Email: ganiyuaa@aceondo.edu.ng …

Read More

Highlights

Abstract

This paper examines the approximate solution of general first order stochastic differential equations (SDEs). Two different methods of solution were considered. They include Drift-implicit Euler-Maruyama method (DIEMM) and full-implicit Euler-Maruyama method (FIEMM). The two methods were adapted from Explicit Euler-Maruyama method (EEMM). Two problems in the form of first order SDEs considered are Black-Scholes option price model (BSOPM) with a drift and without a drift function. The absolute errors were calculated using the exact solution and numerical solution for stepsizes 2^-4, 2^-5, 2^-6, 2^-7, 2^-8, 2^-9.   Comparison in performance of the methods was achieved using mean absolute error criterion. The mean absolute error was then used to determine the order of convergence for each method. The order of convergence obtained for DIEMM and FIEMM was compared with that obtained using EEMM. The results showed that the performance of EEMM was better than DIEMM while the performance of FIEMM was better than that of EEMM and DIEMM for first problem. It was noted that the order of convergence of EEMM and DIEMM are approximately the same in the second problem. This can be associated with the absence of Drift function in second problem. However, FIEMM outperformed EEMM and DIEMM. This is because its order of convergence was less than that of EEMM and DIEMM for second problem. Also, the graphical solutions were constructed for each method can also be identified for stepsize 2^-4.  

Keywords: Stochastic Differential Equations, Itô Lemma, Explicit Euler-Maruyama Method, Drift-Implicit Euler-Maruyama method, Full-Implicit Euler-Maruyama method, Wiener process, Black Scholes Option Price Model, Mean Absolute Error, Order of Convergence.

1. Introduction

Modeling physical systems using Ordinary Differential Equations (ODEs) overlooks stochastic effects. Incorporating random elements into these equations results in Stochastic Differential Equations (SDEs), with the term “stochastic” referring to noise (Rezaeyan and Farnoosh, 2010). A first-order Stochastic Differential Equation is an equation of the specified form.

where f:[0,T]×〖R^n⟶R〗^n is a drift function.
Equation (1.0) can be written as

Where g:[0,T]×〖R^n⟶R〗^(n×m)is the diffusion function. The noise in equation (1.1) is generally called Gaussian white noise. It is expressed as , where is the Wiener process. For the properties of Wiener process see Higham (2001) and Williams (2006) in Ganiyu et al (2015).
Equation (1.1) can be written as

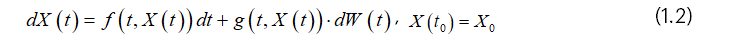
Integrating (1.2) from 0 to t we have

The first integral on the right-hand side of equation (1.3) is known as the Riemann integral, while the second is referred to as the Itô integral or stochastic integral. Numerous researchers have conducted studies on Stochastic Differential Equations (SDEs) of the type described in form (1.2). Among them are Platen (1992), Oksendal (1998), Higham (2001), Burrage et al. (2000), Burrage (2004), Richardson (2009), Anna (2010), Razaaeyan and Farnoosh (2010), Fadugba et al. (2013), Bokor (2003), Sauer (2013), Kayode and Ganiyu (2015), Kayode et al. (2016), Ganiyu et al. (2018), and Ganiyu et al. (2021a).

The aim of this paper is to find the numerical solution of stochastic differential equations using two methods. The methods are drift-implicit Euler-Maruyama and full-implicit Euler-Maruyama methods. The objectives are; to use each of the method aforementioned to determine the approximate solution of two stochastic differential equations used in option pricing, obtain the absolute error for each of the method from the corresponding exact solution and numerical solution for stepsizes 2^-4, 2^-5, 2^-6, 2^-7, 2^-8, 2^-9. to compare the performance of the methods using mean absolute error criterion and to determine the accuracy of each method using strong order of convergence property.

2. Research Methodology

Numerous methodologies exist for solving SDE (1.2), including the Euler-Maruyama method, Milstein method, explicit strong order one Runge-Kutta method, Heun method, and others. For solving SDE (1.1), the Drift-implicit Euler-Maruyama method (DIEMM) and Full-implicit Euler-Maruyama method (FIEMM) were employed, as utilized by Wang and Liu (2009). Their outcomes were benchmarked against results from the Explicit Euler-Maruyama method (EEMM), referenced in the studies by Kayode et al. (2016) and Ganiyu et al. (2018). Additionally, Higham (2001) applied the EEMM in the context of an autonomous system of first-order stochastic differential equations.

The EEMM derived by Kayode et al (2016) is of the form

According to Wang and Liu (2009), the EEMM in equation (2.1) can made implicit by introducing implicitness in the term δtf (ꞇ_j, X_j) giving rise to drift-implicit Euler-Maruyama method (DIEMM)

By introducing implicitness in the second function at the right hand side of equation (2.2), this gives full-implicit Euler-Maruyama method (FIEMM).

2.1 Implementation of the Methods

The method in equation (2.1) was considered by Higham (2001) for EEMM using backward difference. In this paper, we shall apply the two methods (2.2) and (2.3) to SDE (1.2) using discritised interval [0,Ͳ] as 0< ꞇ₁< ꞇ₂<…<ꞇ_j+1=Ͳ. Let δt=Ͳ/L be the stepsize defined as δt=ꞇ_j+1,- ꞇ_j, where N are some integer and ꞇ_j=jδt. The δt-space path increment dW_j=W_j– W_j-1 will be approximated by summing the underlying dt -space increments as established by Higham (2001) using

Wiener increment dW will be generated in MATLAB over the space intervals by using dW:=sqrt (dt)*rand (1,N). For computational purpose, we shall assume that R=1, Dt=R*dt and L=N/R The exact and numerical solution will be obtained using MATLAB software program.

2.2 Mean Absolute Error Criterion

In assessing the accuracy of any numerical method, it is essential to consider the properties of the solution produced by such a method. A key property of SDEs is the convergence of the solution method employed. The convergence issue of SDEs has been explored by numerous researchers, including Higham (2001), Burrage (2004), Beretta et al. (2000), Lactus (2008), Sauer (2013), Fadugba et al. (2013), Kayode and Ganiyu (2015), Kayode et al. (2016), Ganiyu et al. (2018), Ganiyu et al. (2021a), and Ganiyu et al. (2021b), among others.

The convergence of a method of solution of SDEs depends on the magnitude of the mean or expected value of the absolute error being measured. This can be defined as follows.  Suppose a stochastic differential equation of the form (1.2) is given. Suppose further that X(t) and X^h(t) (where h=δt is the stepsize) represent the true solution and numerical approximation of the SDE respectively, the absolute error ‘E’ is defined by

The absolute error in any experiment shall be investigated by chosen the stepsize δt=2^-4

The mean absolute error (MAE) E^h is defined by

where E represent the mean or the expected value.

The Strong order of convergence (SOC) of each method is determined by considering the mean absolute error for six stepsizes, 2^-4, 2^-5, 2^-6, 2^-7, 2^-8, 2^-9.

Remark 2.1

The accuracy of a solution method is gauged by its Mean Absolute Error (MAE). From a list comparing the MAE values of different methods, the one with the lowest MAE is considered to be the most accurate. Additionally, the performance and accuracy of a solution method can be evaluated by identifying which method exhibits the lowest Strong Order of Convergence (SOC).

3. Solution of First Order Stochastic Differential Equations Using Drift-Implicit and Full Implicit Euler-Maruyama Methods

In this section, two problems in the form of first order stochastic differential equation (1.1) will be considered. The two methods (2.2) and (2.3) will be applied to find the approximate solution of the SDEs. The targeted problems are stated below.

Problem 1

where  σ=0.0002 and μ=0.0001 are arbitrary values.

The exact solution of the SDE (3.1) is

Problem 1 is the Black-Scholes option price model with a drift function μX(t) and diffusion function σX(t). The problem was also used by Higham (2001) and Sauer (2013).

Problem 2

where  σ=0.0001 is an arbitrary value.

The exact solution of the SDE (3.3) is

Problem 2 is the Black-Scholes option price model without a drift function but with diffusion function σX(t). In carrying out our numerical experiment, the stepsizes considered are 2^-4, 2^-5, 2^-6, 2^-7, 2^-8, 2^-9. It is assumed that X₀=1 for each of the problem.

The numerical solution of the given problems in (3.1) and (3.3) can then be determined using DIEMM and FIEMM. For the study of solution to first order Stochastic Differential Equations using Explicit Euler-Maruyama Method (EEMM) for Problem 1 as well as simulation curve associated with the method see Ganiyu et al (2018).

3.1 Solution of First Order Stochastic Differential Equations using Drift Implicit Euler-Maruyama Method (DIEMM) For Problem 1

Applying DIEMM of equation (2.2) to problem1 gives

Table 1: Result of using DIEMM (3.5) for solution of Problem 1 with h= 2^-4

The mean absolute error (E^h) is 7.484290742709731e-010.

Table 1 shows the exact solution and numerical solution of problem 1 using DIEMM with stepsize 2^-4. The mean absolute error for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be similarly determined.

Figure 1 shows the sample path of the exact solution and numerical solution of problem 1 using DIEMM. The graphical solution for other stepsizes, 2^-6, 2^-7, 2^-8, 2^-9 can be obtained in a similar manner.

3.2 Solution of First Order Stochastic Differential Equations using Full-Implicit Euler-Maruyama Method (FIEMM) for Problem 1

Applying FIEMM of equation (2.3) to problem 1 gives

Table 2: Result of using FIEMM (3.6) for solution of Problem 1 with h= 2^-4

The mean absolute error (E^h) is 4.074086257244148e-009.

Table 2 shows the exact solution and numerical solution of problem 1 using FIEMM with stepsize 2^-4. The mean absolute error for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be similarly determined.

Figure 2 shows the sample path of the exact solution and numerical solution of problem 1 using FIEMM. The graphical solution for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be obtained in a similar manner.

3.3 Solution of First Order Stochastic Differential Equations using Drift Implicit Euler-Maruyama Method (DIEMM) For Problem 2

Applying DIEMM of equation (2.2) to problem 2 gives

Table 3: Result of using DIEMM (3.7) for solution of Problem 2 with h= 2^-4

The mean absolute error (E^h) is 1.162394613896112e-009.

Table 3 shows the exact solution and numerical solution of problem 2 using DIEMM with stepsize 2^-4. The mean absolute error for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be similarly determined.

Figure 3 shows the sample path of the exact and numerical solution of problem 2 using DIEMM. The graphical solution for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be obtained in a similar manner.

Remark 3.1
The result obtained using DIEMM and  EEMM (See Ganiyu et al (2018) for problem 2 are the same, the reason for this is that there exist no drift function to be made implicit in the method.

3.4 Solution of First Order Stochastic Differential Equations using Full-Implicit Euler-Maruyama Method (FIEMM) For Problem 2

Applying FIEMM of equation (2.3) to problem 2 gives

Table 4: Result of using FIEMM (3.8) for solution of Problem 2 with h= 2^-4

The mean absolute error (E^h) is 4.588471202993105e-009.

Table 4 above shows the exact and numerical solution of problem 2 using FIEMM with stepsize 2^-4. The mean absolute error for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be similarly determined.

Figure 4 shows the sample path of the exact and numerical solution of problem 2 using FIEMM. The graphical solution for other stepsizes 2^-5, 2^-6, 2^-7, 2^-8, 2^-9 can be obtained in a similar manner.

4. Comparison of Mean Absolute Error (MAE) of Explicit, Drift-Implicit and Full-Implicit Euler-Maruyama Methods for Solution of First Order SDEs of Problem 1 (P1)

Stepsize	Explicit EMM P1 Kayode and Ganiyu (2015)	Drift Implicit EMM P1	Full Implicit EMM P1
2-4	6.36669439e-010	7.48429074e-010	4.07408626e-009
2-5	1.04921388e-009	1.04294593e-009	4.48671372e-009
2-6	9.69581149e-010	9.70649827e-010	4.40708724e-009
2-7	6.30707042e-010	5.55700275e-010	4.06850471e-009
2-8	2.52163668e-010	2.21823759e-010	3.67923086e-009
2-9	1.14792709e-010	9.61350666e-011	3.54315376e-009

Method	Order of Convergence P1	Residual P1
Explicit EMM Kayode and Ganiyu (2015)	0.54710253	1.09749078
Drift Implicit EMM	0.63736669	1.03290638
Full Implicit EMM	0.05660868	0.13288578

Stepsize	Explicit EMM P2 Ganiyu et al (2018)	Drift Implicit EMM P2     (New Method1)	Full Implicit EMM P2 (New Method2)
2-4	1.16239446e-9	1.16239461e-009	4.58847120e-009
2-5	1.25768166e-9	1.25768170e-009	4.69481000e-009
2-6	1.07798138e-9	1.07798177e-009	4.51515269e-009
2-7	6.09374184e-10	6.09373751e-010	4.04685462e-009
2-8	2.23838359e-10	2.23838781e-010	3.62954590e-009
2-9	1.05161935e-10	1.05163089e-010	3.52669949e-009

Method	Order of Convergence P2	Residual P2
Explicit EEMM Ganiyu et al (2018)	0.73216346	0.85947327
Drift Implicit EMM	0.73216104	0.85946835
Full Implicit EMM	0.09057947	0.09205844

5. Discussion

In this paper, we have explored two methods for solving general first-order stochastic differential equations (SDEs): the two methods are Drift Implicit Euler Maruyama method (DIEMM) and full implicit Euler Maruyama method (FIEMM). Each of the method was used to determine the numerical solution of two problems used in option pricing. The first problem is with a drift function and the second is without a drift function. The exact solutions of the given stochastic differential equations were determined. This provided the opportunity to obtain the absolute error ‘E’ at time t=[0,Τ] , where T=1. The mean absolute error E^h of each method was calculated to compare the performance of the methods. The mean absolute errors were used to determine the order of convergence of each method. This had provided the opportunity to determine the accuracy of the methods. The results obtained were used to compare the results obtained using explicit Euler Maruyama method (EEMM) by Kayode and Ganiyu (2015) and Ganiyu et al (2018). Our analysis revealed that the order of convergence of the EEMM is less than that of the DIEMM, while the FIEMM’s order of convergence is lower than both the EEMM and DIEMM for the problem 1. However, for the problem 2, the order of convergence of the EEMM closely matches that of the DIEMM, with the FIEMM’s order of convergence still being the lowest. Graphical representations of each method’s solutions were also generated for stepsize 2^-4.  

6.Conclusion

We have analyzed two scenarios involving first-order stochastic differential equations (SDEs). The first scenario addresses the Black-Scholes option pricing model incorporating a drift function, while the second scenario considers the same model but without a drift function. To solve these SDEs, we applied two distinct methodologies: the drift-implicit Euler-Maruyama method (DIEMM) and the full-implicit Euler-Maruyama method (FIEMM). The effectiveness of these methods was evaluated by calculating the absolute errors between the exact solutions and the numerical solutions derived using the aforementioned methods. To compare the performance of the methods, the mean absolute error for each method was obtained using stepsizes 2^-4, 2^-5, 2^-6, 2^-7, 2^-8, 2^-9. The results showed that the accuracy of EEMM is better than that of DIEMM because the order of convergence of EEMM is less than that of DIEMM, while that of FIEMM is better than that of EEMM and DIEMM because its order of convergence (OOC) is less than that of EEMM and DIEMM for problem 1. However, the order of convergence of EEMM is approximately the same as that of DIEMM, while that of FIEMM is more accurate than EEMM and DIEMM because the OOC is less than that of EEMM and DIEMM for problem 2. It can be concluded that the performance of EEMM is better than that of DIEMM, while the performance of FIEMM is better than that of EEMM and DIEMM for problem 1. The order of convergence of EEMM and DIEMM being approximately equal can be associated with the absence of Drift function in problem 2. However, FIEMM outperformed EEMM and DIEMM since its order of convergence was less than that of EEMM and DIEMM for problem 2.

The graphical solutions of each method were constructed for stepsize 2^-4. It can be observed that the graphical solutions of DIEMM and FIEMM are almost the same for problem 1. Similarly, that of DIEMM and FIEMM is almost the same too for problem 2. This confirms the statement credited to Wang and Liu (2009) that there is no simple stochastic counterpart of the Eular method; that is, the method fails because, for example Ε|(1-μδt-σδW_j )^-1|=+∞ for a linear SDE in equation (3.1), nevertheless, the treatment could be to look at a higher-order explicit Strong method like the Milstein method and try to introduce implicitness there (this is for future research).

Conflict of Interest

The research was completed with no conflict of interest.

References

Anna N. (2010). Economical Runge-Kutta Methods with week Second Order for Stochastic Differential Equations. Int. Contemp. Maths. Sciences, 5(24), 24 1151-1160.

Beretta, M., Carletti, F. and Solimano F. (2000). “On the Effects of Environmental Fluctuations in Simple Model of Bscteria- Bacteriophage Interaction, Canad. Appl. Maths. Quart. 8(4) 321-366.

Bokor R.H. (2003). “Stochastically Stable One Step Approximations of Solutions of Stochastic Ordinary Differential Equations”, J. Applied Numerical Mathematics 44, 21-39.

Burrage, K. (2004). Numerical Methods for Strong Solutions of Stochastic Differential Equations: An overview. Proceedings: Mathematical Physical and Engineering Science, Published by Royal Society, 460(2041), 373-402.

Burrage, K. Burrage, P. and Mitsui T. (2000). Numerical Solutions of Stochastic Differential Equations-Implementation and Stability Issues. Journal of Computational & Applied Mathematics, 125, 171-182.

Fadugba S.E., Adegboyegun B.J., and Ogunbiyi O.T. (2013). On Convergence of Euler-Maruyama and Milstein Scheme for Solution of Stochastic Differential Equations. International Journal of Applied Mathematics and Modeling@ KINDI PUBLICATIONS. 1(1), 9-15. ISSN: 2336-0054.

Ganiyu A.A., Olademo J.O. and Fakunle I. (2015). “On The Analytical Solution of Black Scholes Option Price Model (BSOPM) with and with No Drift”. ERJANSS Research Journal. 1(1), 208-220.

Ganiyu A.A., Famuagun K.S. and Akinremi O.V. (2018). “Numerical Solution of Stochastic Differential Equations, Using Explicit EULER-MARUYAMA method. Nigerian Journal of Technological Research. 13(20), 1-20.

Ganiyu A.A., Augustine A.C. and Olademo J.O.A. (2021a). On Heun’s Method for Solution of Scalar Stochastic Differential Equations Journal of Science and Science Education (JOSSEO). 10(1), June 2021 ISSN: 0775-1353 Pp 9-20.

Ganiyu A.A., Kayode S.J. Lawal M.O. and Oluwafemi E.A. (2021b). On Explicit Strong Order One Runge-Kutta Method for Solution of Scalar First Order Stochastic Differential Equations. Journal of Transactions of the Nigerian Association of Mathematical Physics,   Vol. 16, (July-Sept. 2021 Issue) Pp 211-220.

Higham D.J. (2001). An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Review, 43(3), 525-546.

Kayode S.J. and Ganiyu A.A. (2015). “Effect of Varying Stepsize in Numerical Approximation of Stochastic Differential Equations Using One Step Milstein Method. Applied and Computational mathematics 4(5): 351-362. doi.1011648/J.acm.20150405.14

Kayode S.J., Ganiyu A.A. and Ajiboye A.S. (2016). “On One-Step Method of Euler-Maruyama Type for Solution of Stochastic Differential Equations Using Varying Stepsizes. Open Access Library Journal, 3:e2247. http://dx.doi.org/10.4236/oalib.1102247.

Lactus, M.L. (2008). Simulation and Inference for Stochastic Differential Equations with   R Examples. Springer Science + Buisiness Media, LLC, 233 Springer Street, New York, NY10013, USA. Pp 61-62.

Oksendal B. (1998). Stochastic Differential Equations. An Introduction with Application, FifthzEdition, Springer-Verlage, Berlin, Heidelberge, Italy.

Platen E. (1992). An Introduction to Numerical Methods of Stochastic Differential equations. Acta Numerica, 8, 197-246.

Rezaeyan R. and Farnoosh R. (2010). Stochastic Differential Equations and Application of Kalman-Bucy Filter in Modeling of RC Circuit. Applied Mathematical Sciences, Stochastic Differential Equations 4(33), 1119-1127.

Richardson M. (2009). Stochastic Differential Equations Case Study. (Unpublished).

Sauer T. (2013). Computational Solution of Stochastic Differential  Equations. WIRES Comput Stat. doi: 10.1002/wics.1272.

Wang P. and Liu Z. (2009). “Stabilized Milstein Type Methods for Stiff Stochastic Systems”. Journal of Numerical Mathematics and Stochastics, Eulidean Press, LLC. 1(1): 33-34.

Williams C. (2006). A tutorial Introduction to Stochastic Differential Equations: Continuous-time Gaussian Markov Process, Institute for Adaptive and Neural Computation, School of Informatics, University of Edinburgh.

About this Article

Cite this Article

APA

Ganiyu A. A., Kayode S. J., Augustine  A. C., & Fakunle  I. (2024). On Drift-Implicit and Full-Implicit Euler-Maruyama Methods for Solution of First Order Stochastic Differential Equations. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.

Chicago

Ganiyu A. A., Kayode S. J., Augustine  A. C., & Fakunle  I. 2024. “On Drift-Implicit and Full-Implicit Euler-Maruyama Methods for Solution of First Order Stochastic Differential Equations.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.

Corresponding Author Email: famuagunks@aceondo.edu.ng

Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.

Distributed under Creative Commons CC-BY 4.0

Share this article

Use the buttons below to share the article on desired platforms.