Fakunle I.;1 , Arawomo P.O.;2 , Idiong U.S.;3 , Akinremi B.V.;3 & Famuagun K.S.3
1Adeyemi Federal University of Education, Ondo State, Nigeria
*Corresponding Author Email: fakunlei@aceondo.edu.ng …
Highlights
Abstract
In this paper, Hyers-Ulam stability of non-homogeneous nonlinear second order differential equations are consid- ered. Conditions are stated to transform nonlinear second order differential equations to integral inequalities for easy application of Gronwall-Bellman-Bihari inequality. Our results improved and extended some known results in the literature.
Keywords and phrases: Nonlinear differential equation, integral inequality, Hyers-Ulam stability, Gronwall-Bellman-Bihari inequality.
1. Introduction
The purpose of this paper is to study Hyers-Ulam stability of the following equations:
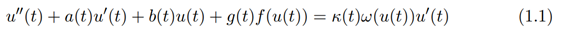
and
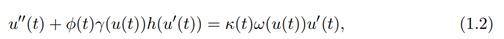
for all t > 0, with initial conditions
Where g:[0,T]×〖R^n⟶R〗^(n×m)is the diffusion function. The noise in equation (1.1) is generally called Gaussian white noise. It is expressed as , where is the Wiener process. For the properties of Wiener process see Higham (2001) and Williams (2006) in Ganiyu et al (2015).
Equation (1.1) can be written as
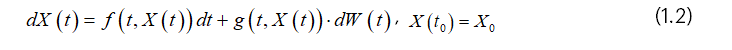
Integrating (1.2) from 0 to t we have

where a(t), b(t), κ(t), φ(t), g(t) ∈ C(R+), f(u), γ(u), ω(u), h(u) ∈ C(R+,R+).
The study of stability for various functional equations originated from a famous talk of Ulam, 1960 who posed a problem concerning the stability of functional equations:” Give conditions in order for a linear function near an approximately linear function to exist”. Since then, this question has attracted the attention of many researchers. Note that the solution to this question was given by Hyers, 1941 for additive functions defined on Banach space in 1941. Thereafter, the result by Hyers 1941, was generalised by Rassias 1978, Aoki, 1950 and Bourgin, 1988. After that, many authors extended the Ulam problem to other functional equations in various directions. In 1998, Alsina and Ger investigated the Hyers-Ulam stability of a differential equation. They have proved that for every differentiable mapping f:I→R satisfying |f(x)-f(x)| ≤∈ for every x∈I I, where ∈ > 0 is a given number and I is an open interval of R, there exists a differentiable function g:I→R with property g‘ (x)=g(x) and |f(x)-g(x)| ≤ 3∈ for all x∈I. The result of Alsina and Ger, 1998 was extended by Miura et al., 2003a; Miura et al., 2003b , Takahasi et al., 2002, and by Takahasi, et al., 2004 to the Hyers-Ulam stability of the first order linear differential equations and linear differential equations of higher order with constant coefficients. Furthermore, Jung, 2006a; Jung, 2006b; Jung, 2004; Jung 2005 has obtained result on the stability of linear differential equations extending the results of Takahash et al., 2004. Rus, 2010a; Rus, 2010b has proved some results on the stability of linear differential and integral equations using Gronwall’s lemma and the technique of weakly Picard operators.
Recently, Wang, et al., 2008 and Li & Shen 2010 proved the Hyers-Ulam stability of the linear differential equations of the first order and the linear differential equations of the second order with constant coefficients by using the method of integral factor.
Many of the authors prefer to consider the Hyers-Ulam stability of linear differential equations due to the fact that it can easily be handled. In this paper, equations (1.1) and (1.2) will be transformed to integral inequalities using the conditions that we shall prescribe for application of Gronwall-Bellman-Bihari inequality to study the Hyers- Ulam stability. The results established in this paper through Gronwall-Bellman-Bihari inequality extended some of the results in the literature.
2. Preliminary
First of all, we give some definitions, lemmas and theorems which are going to assist us in this work.
2.1.1 Definition 1
We say that equation (1.1) has the Hyers-Ulam stability, if there exists a constant K1*≥0 with the following property: for every ϵ > 0, u(t) ∈ C2(R+), if
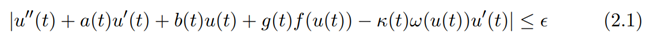
then, there exists some u0(t) ∈ C2(R+) such that
|u(t) − u0(t)| ≤ K1∗ϵ.
We call such K1* a Hyers-Ulam constant.
2.1.2 Definition 2
Equation (1.2) is Hyers-Ulam stable, if given ϵ > 0 and there exists a solution u(t) ∈ C2(R+), such that
|ujj(t) + φ(t)γ(u(t))h(uj(t)) − κ(t)ω(u(t))uj(t)| ≤ ϵ,) (2.2)
in addition, there exists positive K2* and any solution u0 (t)∈C2 R+ of the (1.2) with initial condition (1.3) such that
|u(t) − u0(t)| ≤ K2∗ϵ,
We call such K2∗ Hyers-Ulam constant for the differential equation (1.2).
2.1.3 Definition 3
A function ω: [0, ∞) → [0, ∞) is said to belong to a class Ψ
if
- ω(u) is nondecreasing and continuous for u ≥ 0
- ω(u) ≤ ω(v/u)for all u and v ≥ 1
- there exists a function φ, continuous on [0, ∞) with ω(αu) ≤ φ(α)ω(u) for α ≥ 0
2.2 Lemma 1: Bihari, 1957.
Let u(t), f(t) be positive continuous functions defined on a ≤ t ≤ b,(≤ ∞) and K > 0, M ≥ 0, further let ω(u) be a nonnegative nondecreasing continuous function for u ≥ 0, then the inequality
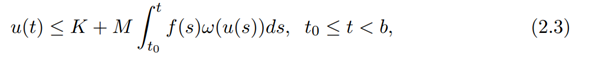
implies the inequality
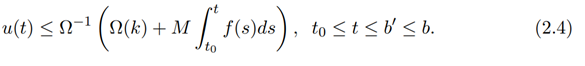
Where
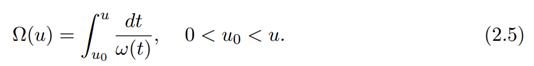
In the case ω(0) > 0 or Ω(0+) is finite, one may take u0 = 0 and Ω−1 is the inverse function of Ω and t must be in the subinterval [t0, b0 ] of [t0, b] such that
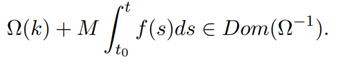
2.2.1 Theorem 1: (Murray, 1974)
If f(t) and g(t) are continuous in [t0, t] ⊆ I and f(t) does not change sign in the interval, then there is a point ξ ∈ [t0, t] such that
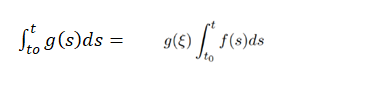
2.2.2. Theorem 2: Fakunle and Arawomo, 2018a; Fakunle and Arawomo, 2018b; Fakunle and Arawomo, 2022a; Fakunle and Arawomo, 2022b.
Suppose u(t), r(t), h(t) ∈ C(I, R+) and $(u), β(u) ∈ Ψ be nonnegative, monotonic, nondecreasing, continuous and ω(u) be a submultiplicative for u > 0.
Let
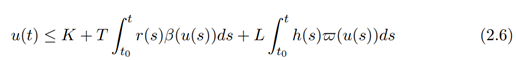
for K, T and L positive constants, then
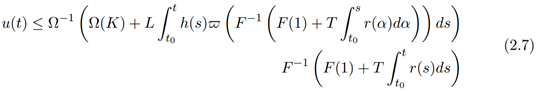
where β(u) 6= $(u), Ω is defined in equation (2.5) and F(u) is defined as
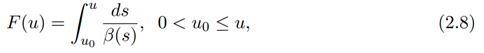
Where F−1, Ω−1 are the inverses of F, Ω respectively and t is in the subinterval (0, b) ∈ I so that
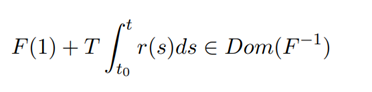
and
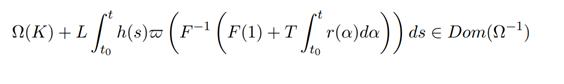
3. Main Results
In this section, we establish the Hyers-Ulam stability of the nonlinear differential equations (1.1), (1.2) as follow: Theorem 3. Assume the following conditions
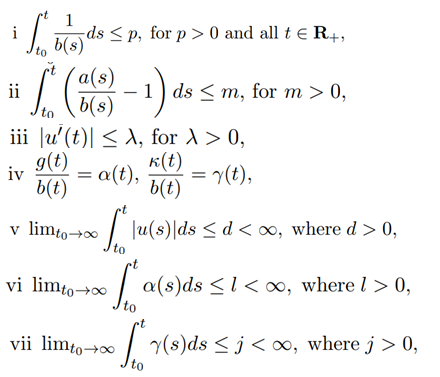
are satisfied and γ, α ∈ C(R+). In addition, let f, ω ∈ Ψ be continuous, nondecreasing and monotonic, then equation (1.1) has the Hyers-Ulam stability and Hyers-Ulam constant is given as
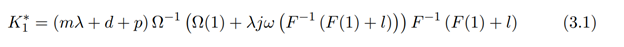
Proof
Evaluating the inequality (2.1) we have
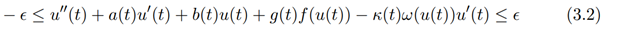
It is clear that
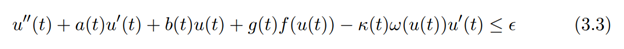
Let
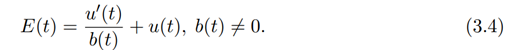
We obtain
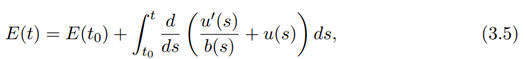
Using equation (1.3), we have
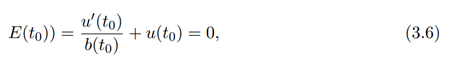
It follows from equation (3.5) that
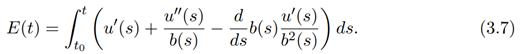
Since b(t) is an increasing function, then d dsb(t) ≥ 0, equation (3.7) reduced to
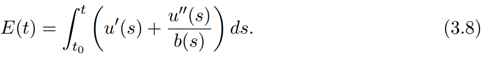
Substituting for u 00(t) in equation (3.8) by using equation (3.3), we have
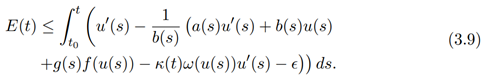
Simplifying equation (3.9), we obtain
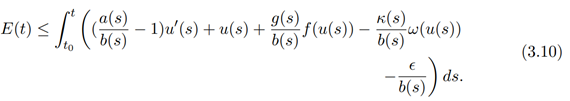
It is clear from equation (3.4) that

Using inequality (3.11) in inequality (3.10), we have
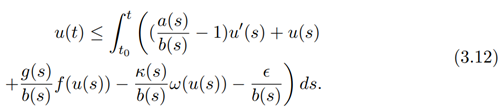
Expressing equation (3.12) further, we obtain
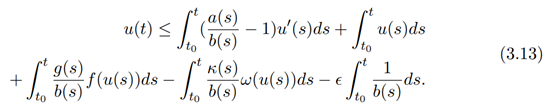
Taking the absolute value of both sides, we have
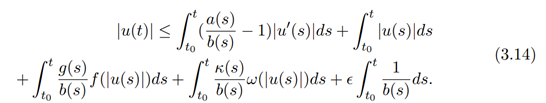
It follows from (3.14) that
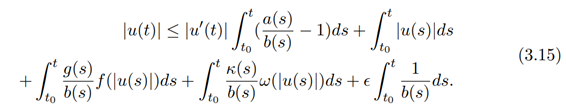
Using the conditions (i-v), we get
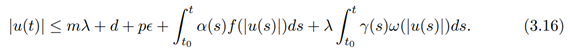
Simplifying equation (3.16) further we have
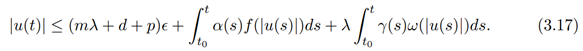
Applying Theorem 2, we obtain
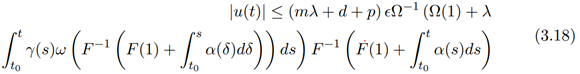
Applying the conditions (vi)- (vii), we arrive at
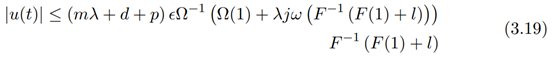
Hence,
Therefore,
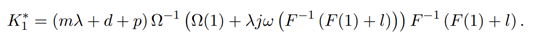
3.1.1 Theorem 4
Let u(t) ∈ C 2 (I, R+) satisfies the differential inequality (2.2) for all t ∈ I and for some > 0, then there exists a solution u0(t) ∈ C 2 (I, R+) of equation (1.2) such that
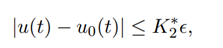
provided the following conditions are satisfied:
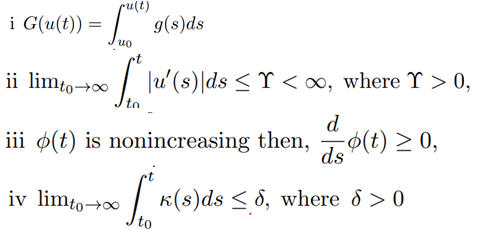
Proof
From equation (2.2), we get
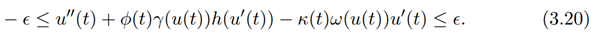
It is clear that
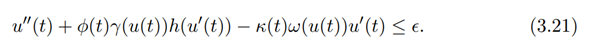
Multiplying equation (3.21) by u 0 (t) and integrating from t0 to t, we obtain
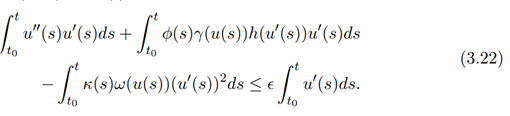
Using equation (1.3), we get
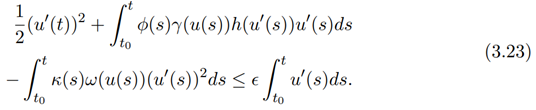
By Theorem 1 there exists ι, µ ∈ [t0, t] such that
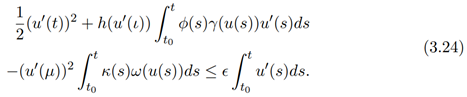
By condition (i) we obtain
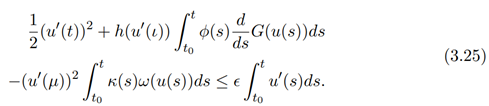
Integrating by part using condition (iii) we have
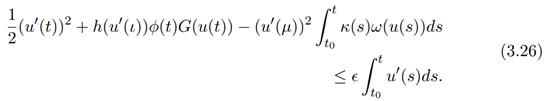
Put
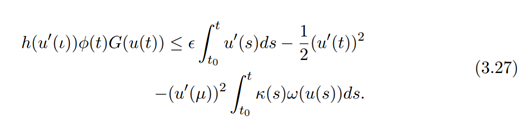
Taking the absolute value of both sides, we have
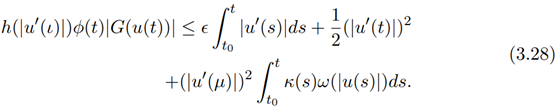
Using condition (iii) of Theorem 3 and condition (ii) of Theorem 4, we get
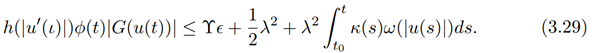
Setting h(|u 0 (ι)|)φ(t)|G(u(t))| ≥ |u(t)|, we obtain
Applying Theorem 1
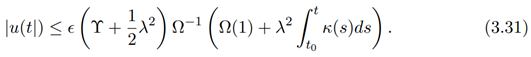
Using the condition (iv), we obtain
Hence,
Therefore,
Example 1:
Consider the following equation
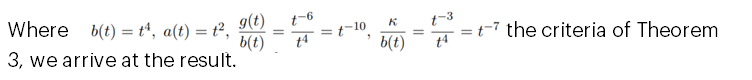
Example 2:
Consider the following equation
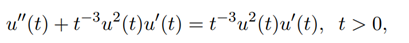
Using the criteria of Theorem 4, we arrive at the result.
Acknowledgement
I acknowledged all reviewers who have been appointed to review this paper.
References
Abdollahpour, A., & Najati, A. (2011). Stability of linear differential equations of third order. Applied Mathematics Letters, 24, 1827-1830.
Alsina, C., & Ger, R. (1988). On some inequalities and stability results related to the exponential function. Journal of Inequalities and Applications, 2, 373-380.
Aoki, T. (1950). On the stability of the linear transformation in Banach spaces. Journal of Mathematical Society of Japan, 2, 64-66.
Bihari, I. (1957). Researches of the boundedness and stability of the solutions of nonlinear differential equations. Acta Mathematica Academiae Scientiarum Hungaricae, 7, 278-291.
Bourgin, D. G. (1988). Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society, 57, 223-237.
Fakunle, I., & Arawomo, P. O. (2018a). Hyers-Ulam stability of certain class of nonlinear second order differential equations. International Journal of Pure and Applied Mathematical Sciences, 11(1), 55-65.
Fakunle, I., & Arawomo, P. O. (2018b). On Hyers-Ulam stability of nonlinear second order ordinary and functional differential equations. International Journal of Differential Equations and Applications, 17(1), 77-88.
Fakunle, I., & Arawomo, P. O. (2019). Hyers-Ulam stability of a perturbed generalised Lienard equation. International Journal of Applied Mathematics, 32(3), 479-489.
Fakunle, I., & Arawomo, P. O. (2022a). Hyers-Ulam-Rassias stability of a certain perturbed nonlinear Lienard type differential equation. To appear in IAENG International Journal of Applied Mathematics.
Fakunle, I., & Arawomo, P. O. (2022b). Hyers-Ulam-Rassias stability of nonlinear second order of a perturbed ordinary differential equation. To appear in Proyecciones Journal of Mathematics.
Hyers, D. H. (1941). On the stability of the linear functional equation. Proceedings of the National Academy of Science of the United States of America, 27, 222-224.
Jung, S.-M. (2004). Hyers-Ulam stability of linear differential equations of first order. Applied Mathematics Letters, 17, 1135-1140.
Jung, S.-M. (2005). Hyers-Ulam stability of linear differential equations of first order (III). Journal of Mathematical Analysis and Applications, 311, 139-146.
Jung, S.-M. (2006a). Hyers-Ulam stability of linear differential equations of first order (II). Applied Mathematics Letters, 19, 854-858.
Jung, S.-M. (2006b). Hyers-Ulam stability of a system of first order linear differential equations with constant coefficient. Journal of Mathematical Analysis and Applications, 320, 554-561.
Li, Y., & Shen, Y. (2010). Hyers-Ulam stability of linear differential equation of second order. Applied Mathematics Letters, 23, 306-309.
Miura, T., Miyajima, S., & Takahasi, S. E. (2003a). A characterisation of Hyers-Ulam stability of first order linear differential operators. Journal of Mathematical Analysis and Applications, 286, 136-146.
Miura, T., Miyajima, S., & Takahasi, S. E. (2003b). Hyers-Ulam stability of linear order differential operators with constant coefficient. Journal of Mathematical Analysis and Numerical Methods, 258, 90-96.
Rassias, T. H. M. (1978). On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society, 72(2), 297-300.
Rus, I. A. (2010). Ulam stability of ordinary differential equation. Studia Universitatis Babes-Bolyai Mathematica, 54(4), 306-309.
Rus, I. A. (2010). Ulam stability of ordinary differential equations in a Banach space. Carpathian Journal of Mathematics, 126, 103-107.
Schum, R. S. M. (1974). Outline of theory and problems of calculus (SI Metric Edition, International ed.).
Takahasi, S. E., Miura, T., & Miyajima, S. (2002). On the Hyers-Ulam stability of the Banach space-valued differential equation y’ = λy. Bulletin of the Korean Mathematical Society, 39(2), 309-315.
Takahasi, S. E., Takagi, H., Miura, T., & Miyajima, S. (2004). The Hyers-Ulam stability constants of first order linear differential operators. Journal of Analysis and Applied Mathematics, 296, 403-409.
Ulam, S. M. (1960). Problems in modern mathematics (Science Editions, Wily, New York, NY, USA, Chapter 6).
Wang, G., Zhou, M., & Sun, L. (2008). Hyers-Ulam stability of linear differential equations of first order. Applied Mathematics Letters, 21, 1024-1028.
About this Article
Cite this Article
APA
Fakunle I., Arawomo P.O., Idiong U.S., Akinremi B.V. and Famuagun K.S. (2024). On Hyers-Ulam Stability of Non-homogeneous Nonlinear Second Order Differential Equations. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.
Chicago
Fakunle I., Arawomo P.O., Idiong U.S., Akinremi B.V. and Famuagun K.S. 2024. “On Hyers-Ulam Stability of Non-homogeneous Nonlinear Second Order Differential Equations.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.
Received
22 March 2024
Accepted
12 May 2024
Published
30 May 2024
Corresponding Author Email: famuagunks@aceondo.edu.ng
Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.
Distributed under Creative Commons CC-BY 4.0
Share this article
Use the buttons below to share the article on desired platforms.