Application of Garch, TS-Garch and GJK-Garch Models in Modelling Volatility in Farm Produce Inflation in Nigeria

Ogunbona B. D.;¹ , Osho F. T.;² & Hairullahi M. U.³

¹Adeyemi Federal University of Education, Ondo State, Nigeria

*Corresponding Author Email: ogunbonabd@aceondo.edu.ng …

Read More

Highlights

Abstract

Over the past two decades, Nigeria has experienced a significant rise in the price level of farm produce, attributed to political instability and government policies. In the field of economic research, ARIMA, ARCH, and GARCH models have been traditionally employed to model the volatility of farm produce inflation in Nigeria. However, a comparative analysis examining the modeling capacities of GARCH, TS-GARCH, and GJK-GARCH has not been conducted, which this paper aims to address. The objective is to identify which among these three models most effectively captures the volatility in farm produce inflation in Nigeria. This study focuses on comparing the modeling capabilities of Symmetric GARCH (Generalized Autoregressive Conditional Heteroskedasticity) and Asymmetric GARCH models for farm produce inflation in Nigeria. We employed GARCH (1,1), TS-GARCH (Threshold GARCH) (1,1), and GJK-GARCH (Glosten-Jagannathan-Runkle GARCH) (1,1) models to model the volatility of major crops using time series data from 2009 to 2022. The Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) were utilized as metrics to assess the performance of these models, with the model demonstrating the lowest AIC and BIC values considered the most effective. The findings indicated that Asymmetric GARCH models, which account for the possibility that positive and negative shocks to financial markets have different effects on volatility, outperformed the Symmetric GARCH model. Among the three models analyzed, the TS-GARCH model emerged as the most accurate for modeling farm produce inflation in Nigeria. This conclusion underscores the importance of incorporating asymmetries in the volatility modeling of agricultural commodity prices, providing valuable insights for policymakers, investors, and researchers concerned with agricultural economics in Nigeria.

Keywords: GARCH, TS-GARCH, GJK-GARCH, Farm Produce, Inflation, Volatility.

1. Introduction

IGI Global characterizes farm produce as raw agricultural products derived from farming activities, including vegetables, fruits, flowers, and livestock intended for human consumption. The issue of rising food prices has emerged as a significant concern for governments in many developing countries. In nations like Nigeria, where poverty rates are high, the escalating cost of food exacerbates the poverty situation (Nzeh et al., 2023). Modeling farm produce inflation is crucial for farmers and agricultural policymakers to enhance production planning decisions. Farm produce frequently experiences price fluctuations, a phenomenon observed by various researchers (Antwi et al., 2021; Kumari et al., 2019; Nigatu & Adjemian, 2020; Nugroho et al., 2018). Von Braun and Tadesse (2012) in Lestari et al., (2022) noted that natural factors often cause agricultural commodity prices to fluctuate.

Volatility refers to rapid price changes within a specific year (Rauch et al., 2019). Omotosho and Doguwa (2013) in Ogenyi and Umeh (2019) mentioned that, in statistical terms, volatility is often referred to as variance, measuring the dispersion of a random variable from its mean value. Therefore, inflation volatility concerns the fluctuation or instability in a selected inflation measure, with the timing of volatility being unpredictable (Wang et al., 2019; Yip et al., 2020). Price fluctuations can have a positive impact on inflation (Babihuga & Gelos, 2015), with larger changes potentially increasing price volatility. The greater the volatility, the higher the uncertainty regarding future prices (Fameliti & Skintzi, 2022; He & Serra, 2022). Pilbeam et al. (2015) in Youssef and Rowen (2021) described volatility as the standard deviation or variance of the returns of an asset over a specific period. Brooks (2014) in Nybo (2020) stated that volatility data exhibit non-linear characteristics such as leptokurtosis, clustering, and leverage effects, defining leptokurtosis as the increased likelihood of volatility data containing extreme outliers. Volatility clustering indicates the tendency for large changes in asset returns to be followed by more substantial changes, while the leverage effect describes how negative price movements result in higher volatility compared to an equivalent positive movement.

Modeling volatility has become an important research area in recent years, typically employing analytical and historical approaches. The analytical method assumes a distribution, whereas the historical approach deals with the empirical distribution of past information (Njagi et al., 2018). Many agricultural commodity price data are inherently noisy and volatile, responding quickly to actual and perceived changes in supply and demand conditions, with weather-induced fluctuations in farm production exacerbating the situation. To address volatility, the Autoregressive Conditional Heteroscedastic (ARCH) model proposed by Engle (1982) has become popular. Bollerslev (1986) generalized this model into the Generalized ARCH (GARCH) model for a more parsimonious representation of ARCH (Achal et al., 2015). The GARCH model, a statistical model for modeling volatility in time series data, is a type of autoregressive model that accommodates time-varying variance, thus known as variance function models. Standard GARCH models are symmetric, only modeling scenarios where effects of high and low volatility on farm produce inflation are the same. Over time, asymmetric GARCH models, such as Exponential GARCH (E-GARCH), Glosten Jagannathan and Runkle GARCH (GJK-GARCH), TS-GARCH, and T-GARCH, have been developed to address volatility in farm produce inflation more effectively. This paper is organized as follows: section 2 reviews previous literature; section 3 discusses the methodology; section 4 presents the general results, and section 5 concludes the paper.

2. Literature Review

Autoregressive Conditional Heteroscedasticity (ARCH) and Generalized Autoregressive Conditional Heteroscedasticity (GARCH) models have been instrumental in many studies aiming to estimate farm produce inflation. Engle introduced the ARCH model in 1982, which was later generalized by Bollerslev in 1986. Lim and Sek (2013) mentioned that several extensions of these models have been proposed to enhance the estimation of volatility. Among these GARCH variants are GARCH-M, IGARCH, EGARCH, Threshold GARCH, Asymmetric GARCH (AGARCH), TS-GARCH, and Fractionally Integrated GARCH (FIGARCH).

A substantial body of literature has focused on using the GARCH model to analyze volatility in food, agricultural products, or farm produce. Ogenyi and Umeh (2019) employed the ARCH and GARCH models to analyze the determinants of inflation volatility in Nigeria from 1980 to 2010. Their findings indicated that variables such as past inflation, Gross Domestic Product (GDP), government expenditure, government debt stock, imports, exports, and exchange rates contributed to inflation volatility during the study period. Conversely, unemployment and interest rates from previous years were found to significantly reduce inflation volatility in Nigeria.

Ajibade et al. (2020) measured the volatility in prices of staple foods using the GARCH approach and explored the driving factors behind this volatility from 1970 to 2019. Their analysis revealed persistent volatility in food prices throughout the study period, identifying insurgency, political stability in neighboring countries, trade liberalization, GDP per capita, inflation rate, government effectiveness, crop production, crude oil prices, and exchange rate as key factors influencing food commodity price volatility.

Manasseh et al. (2016) investigated volatility and commodity price dynamics in Nigeria using the GARCH and exponential GARCH models. They also explored the causality direction between domestic commodity prices and the spot price of commodity derivatives. The findings showed that 30% of the volatility in the international commodity market could be explained by the volatility in domestic and international export commodity prices, while international oil spot prices accounted for 7% of the volatility in locally consumed goods and export commodity price index explained 16% of the spot price of international commodities between 2000 and 2013 in Nigeria.

Nasution et al. (2021) in Lestari et al. (2022) observed that certain farm produce, such as chili, are susceptible to volatility similar to currencies. Pilbeam and Langeland (2015) highlighted that despite the extensive literature on volatility forecasting, the determination of the optimal model remains an open question. This ongoing debate underscores the complexity of modeling economic and financial volatility and the necessity for continued research to refine these models for more accurate predictions.

3. Methodology

3.1 Research Design

The GARCH (Generalized Autoregressive Conditional Heteroscedasticity), GJK-GARCH (Glosten-Jagannathan-Runkle GARCH), and TS-GARCH (Taylor-Schwert GARCH) models were utilized to analyze and model the volatility of farm produce inflation in Nigeria.

3.2 Standard Garch-Type Model

The GARCH model, an extension of the ARCH (Autoregressive Conditional Heteroscedasticity) model, provides a comprehensive framework for modeling the changing variance, or volatility, observed in time series data. It presents a more parsimonious approach compared to the higher orders of ARCH models, which may lead to redundancy of variables or multicollinearity. The GARCH (p, q) model is generally given by:

The GARCH (1,1) model is the most commonly used. The form of GARCH (1,1) model is given by:

In order to have a positive variance every time, the following restrictions are imposed: α₀ > 0, and α₁, β₁ ≥ 0. Also, for a good model α₁ + β₁ < 1 in order to have a decaying variance.

3.3 Asymmetric Garch Models

While the standard GARCH model effectively captures volatility clustering and heavy-tailed distributions, its symmetric distribution fails to account for the leverage effect, where negative and positive market movements have different impacts on volatility. To address this limitation, several asymmetric GARCH models have been proposed, including the Taylor-Schwert GARCH (TS-GARCH) model and the Glosten-Jagannathan-Runkle (GJR-GARCH) model, which are considered in this paper.

3.3.1 Taylor-Schwert Garch (TS-GARCH)

The TS-GARCH model specifically addresses the asymmetry in volatility responses and was developed by Taylor and Schwert in 1986 to overcome three primary shortcomings of the symmetric GARCH model. These include its insensitivity to the asymmetric response of volatility, the parameter restrictions needed to ensure the positivity of conditional variance, and challenges in measuring persistence in stationary time series. The TS-GARCH (1,1) models the time-varying standard deviation:

3.3.2 Glosten-Jagannathan-Runkle Garch Model (GJR-GARCH)

The GJR-GARCH model, proposed by Glosten, Jagannathan, and Runkle, incorporates the leverage effect based on the state of past innovations. The GJR-GARCH (1,1) model, while resembling the T-GARCH (1,1), distinctively models time-varying variances. The volatility equation of the GJR-GARCH (1,1) model is structured to reflect this characteristic.

3.4 Model Selection Methods

The model selection methods used in this paper are discussed as follows:

3.4.1 The Akaike Information Criterion (AIC)

The Akaike Information Criterion (AIC), developed by Akaike in 1974, is a statistical method designed to evaluate the adequacy of a model in fitting the data it was derived from. In the realm of statistics, AIC is utilized to compare various models to ascertain which one best fits the data. AIC calculates the best-fit model as the one that explains the most variance with the least number of independent variables. It gauges the relative informational value of a model by combining the maximum likelihood estimate (how accurately the model replicates the data) with the number of parameters (independent variables) the model incorporates. The formula for AIC is:  

The AIC formula is influenced by the number of independent variables used (K) and the log-likelihood estimate (L), indicating the model’s likelihood of producing the observed y-values. According to Bevans (2020), the default value of K is always 2, adjusting upwards based on the number of independent variables employed in the model.

3.4.2 Bayesian Information Criterion (BIC)

The Bayesian Information Criterion (BIC), introduced by Schwarz in 1978, serves as a model selection criterion among a finite set of models, favoring the model with the lowest BIC. Like AIC, BIC is partly founded on the likelihood function and bears similarities to the Akaike information criterion. Adding parameters to a model can increase its likelihood, but may also lead to overfitting. BIC and AIC address this issue by incorporating a penalty for the number of parameters within the model, with BIC imposing a stricter penalty than AIC (Bhat and Kumar, 2010).

The BIC is formally defined as

where

• L= the maximized value of the likelihood function of the model M
• n = the sample size;
• k = the number of free parameters to be estimated.

If the model under consideration is a linear regression, k represents the number of regressors, including the intercept, as noted by Findley (1991). The objective in model selection processes is to minimize either the AIC or BIC values. Generally, larger models will provide a better fit, reflected by smaller Residual Sum of Squares (RSS), but they also incorporate more parameters. Therefore, the optimal model selection seeks to balance the goodness of fit with the size of the model. The BIC tends to penalize larger models more severely compared to the AIC, often leading to a preference for smaller models when using BIC for model selection. Both AIC and BIC are versatile and can be employed as selection criteria across various model types. These criteria do not assess the AIC or BIC for every conceivable model but instead rely on a search method that sequentially compares models for the best fit (Faraway, 1994).

3.4.3 Hannan–Quinn Information Criterion

The Hannan–Quinn Information Criterion (HQIC) serves as an alternative criterion for model selection, alongside the Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC). The HQIC offers a balance between the AIC’s tendency to prefer more complex models and the BIC’s inclination towards simpler models. It is calculated using a formula that, similar to AIC and BIC, includes a penalty for the number of parameters in the model but with a different penalty term size. The HQIC is particularly useful in situations where the sample size is moderate to large, providing a compromise between the likelihood of the model and the complexity of the model in terms of parameter count. The HQIC is less commonly used than AIC and BIC but offers a valuable alternative perspective in model selection, especially in econometric and time series analysis contexts. It is given as      

where,

• L_max = the log-likelihood,
• k = the number of parameters, and
• n = the number of observations.

4. Data Collection and Analysis

4.1 Source of Data

The data for this research was sourced from the Nigeria National Bureau of Statistics (NBS), specifically recorded monthly figures on inflation for All items index excluding farm produce, spanning from 2009 to 2022. This secondary data was extracted from the CPI_REPORT_NOV_2022 published by the National Bureau of Statistics.

4.2 ARCH Effect Identification

The initial analysis of the study aimed to ascertain the stationarity of the data and to detect the presence of Autoregressive Conditional Heteroskedasticity (ARCH) effects. The ARCH effect indicates the presence of heteroskedasticity within the dataset and can be identified by analyzing the p-value from the test for the ARCH effect. An ARCH effect is considered present if the p-value is less than 0.05 (Kumari et al., 2019).

 4.3 Results and Analysis

4.3.1 Stationary Tests before Differencing

Graph of Series before Differencing

Figure 4.1: Time plot of the series before differencing

The time plot of the series provided an initial indication of the characteristics of the Farm Produce time series. Throughout the study period, the Farm Produce exhibited an increasing trend, characterized by fluctuations, suggesting that the mean of the Farm Produce has been changing over time in Nigeria. Therefore, the series is identified as non-stationary.

4.3.2 Unit Root Tests before Differencing

ADF TEST H₀: There is Unit root (the series is not stationary)

Table 4.1: ADF tests before Differencing

TEST	Test Statistics	P-Value
Without constant	4.22971	1.000
With constant	5.40135	1.000

KPSS TEST H₀: The series is stationary.

Table 4.2: KPSS tests before Differencing

Test	Test Statistics	Critical Value
With Trend	2.62065	5% (0.148)
Without trend	0.776412	5%(0.462)

Since the Farm Produce time series is not stationary, we have to make it stationary before we can apply the GARCH methodology. We do this by differencing the series.

4.3.3 Stationary Tests after First Differencing

Graph of Series after First Differencing

Figure 4.2: Time plot of the series after first differencing

4.3.4 Unit Root Tests After First Differencing

ADF Test: H₀ There is Unit root (the series is not stationary)

Table 4.3: ADF Tests after first Differencing

TEST	Test Statistics	P-Value
Without constant	4.22971	2.856e-007
With constant	0.178177	0.9713

KPSS Tests: H₀: The series is stationary

Table 4.4: KPSS Tests after first Differencing

Test	Test Statistics	Critical Value
With trend	0.242302	5% (0.148)
Without trend	1.98742	5% (0.462)

4.3.5 Stationary Tests after Second Differencing

Graph of Series after second Differencing

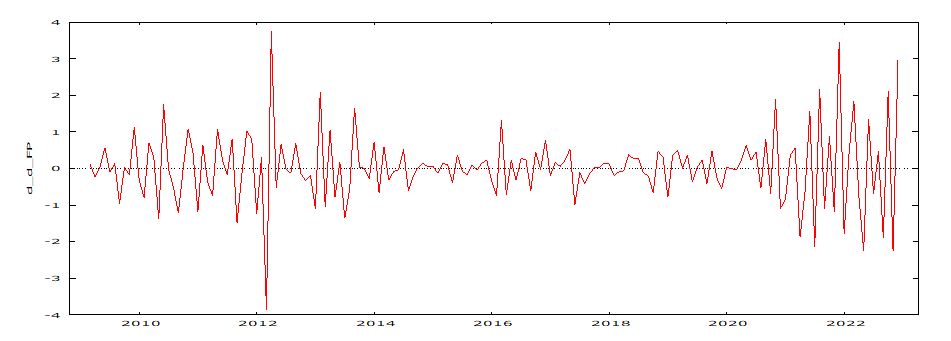
Figure 4.3, which displays the second difference of the Farm Produce series, does not exhibit any trend, suggesting that the second-differenced Farm Produce series might be stationary. This hypothesis is further explored through the formal application of the Augmented Dickey-Fuller (ADF) and Kwiatkowski-Phillips-Schmidt-Shin (KPSS) unit root tests.

Unit Root Tests after second Differencing

ADF Test: H₀ There is Unit root (the series is not stationary)

Table 4.5: ADF Tests after second differencing

TEST	Test Statistics	P-Value
Without constant	-7.13183	1.024e-009
With constant	-6.95539	4.365e-010

KPSS Tests: H₀: The series is stationary

Table 4.4: KPSS Tests after second Differencing

Test	Test Statistics	Critical Value
With trend	0.0159384	5% (0.148)
Without trend	0.0417673	5% (0.462)

The outcomes of the ADF tests, indicated by test statistics falling below the critical regions, lead to the rejection of the null hypothesis. Thus, it is concluded that the time series is stationary, meaning it does not contain a unit root or a stochastic trend. Similarly, the KPSS tests show that all test statistics are below the critical value, allowing us to conclude that the data series has achieved stationarity around a deterministic trend.

4.4 Checking for Volatility Clustering/Arch Effect

4.4.1 Checking for Volatility Clustering

The graph resulting from the second differencing, as shown in Fig.4.3, reveals the presence of volatility clustering, where periods of high volatility are followed by a return to lower volatility levels. This pattern indicates that the fluctuations in the series are not random but exhibit persistence in their volatility.

4.4.2 Test for ARCH effect

Table 4.6: Test for ARCH of order 12

Parameters	Coefficient	Std. Error	t-ratio	P-value
alpha(0)	0.300467	0.211256	1.422	0.1572
alpha(1)	0.472451	0.0865286	5.460	2.09e-07 ***
alpha(2)	−0.183953	0.0948067	−1.940	0.0543   *
alpha(3)	0.152413	0.0958154	1.591	0.1139
alpha(4)	−0.058652	0.0971423	−0.6038	0.5470
alpha(5)	0.167946	0.0979605	1.714	0.0886   *
alpha(6)	−0.07981	0.0987765	−0.8080	0.4205
alpha(7)	0.0942218	0.0991628	0.9502	0.3437
alpha(8)	−0.0483304	0.100599	−0.4804	0.6317
alpha(9)	0.0720543	0.102321	0.7042	0.4825
alpha(10)	0.0382920	0.103001	0.3718	0.7106
alpha(11)	0.143774	0.101875	1.411	0.1604
alpha(12)	0.00689464	0.0926666	0.07440	0.9408

• Null hypothesis: no ARCH effect is present
• Test statistic: LM = 39.9271
• With p-value = P (Chi-square (12) > 39.9271) = 7.39394e-005
• There is ARCH effect since p-value = 7.39394e-005 < 0.05. Presence of ARCH effect means that we can apply GARCH models.

4.4.3 GARCH Model Identification and Selection

Table 4.7: Result of GARCH model selection for the Farm Produce

Model	AIC	SIC	HQC
GARCH (1,1)	241.295	252.478	245.900
TS-GARCH (1,1)	238.670	249.753	243.170
GJR-GARCH (1,1)	240.217	254.070	245.842

The above table shows the three models with their AIC, SIC and HQC. The best model among them is TS-GARCH (1,1) model because it has the minimum AIC, SIC and HQC.

4.4.4. TS-GARCH (1,1) Model Estimation

After the best model has been chosen, the parameters of the model were estimated. The results of this estimate are revealed in the table below:

Table 4.8: Result of TS-GARCH (1,1) model estimation for the Farm Produce

Parameters	Coefficient	Std. Error	Z	P-value
Constant	0.0307300	0.0623562	0.4928	0.6221
Omega	0.0631601	0.0496287	1.273	0.2031
Alpha	0.489208	0.163314	2.995	0.0027 ***
beta	0.589514	0.137029	4.302	1.69e-05 ***

5. Conclusion

Through the analysis conducted, the steps of the GARCH Methodology were meticulously followed. After differencing the Farm Produce data once, it remained non-stationary, as confirmed by formal Augmented Dickey-Fuller (ADF) and Kwiatkowski-Phillips-Schmidt-Shin (KPSS) tests. Proceeding to the second difference, the results of the ADF tests—showing test statistics below the critical values (p-value < 0.05)—led to the rejection of the null hypothesis. Thus, it was concluded that the time series is stationary, exhibiting no trends, seasonal variations, or hidden patterns, and lacks a stochastic trend, potentially suggesting a deterministic trend instead. In the KPSS tests, with test statistics falling below the critical values, the null hypothesis was accepted, indicating that the data series is indeed stationary around a deterministic trend.

The comparison and modeling of the three models under review were conducted using their Akaike Information Criterion (AIC), Schwarz Information Criterion (SIC), and Hannan-Quinn Information Criterion (HQC). This comparison aimed to select the best model, characterized by the minimum values of AIC, SIC, and HQC. The TS-GARCH ARIMA (1,1) model emerged as the most parsimonious and adequate model, featuring the lowest AIC, SIC, and HQC values. Consequently, the conditional variance equation of the TS-GARCH (1,1) model was derived to model the volatility of farm produce inflation in Nigeria effectively.

This analysis underscores the importance of identifying the appropriate model to accurately capture the volatility characteristics of farm produce inflation. The selection of the TS-GARCH ARIMA (1,1) model reflects its superior capacity to model the complex dynamics of farm produce inflation, providing valuable insights for policymakers, economists, and stakeholders within the agricultural sector.

Conflict of Interest

The research was completed with no conflict of interest.

References

Achal L., Girish K. J., Ranjit K. P. and Bishal G. (2015): Modelling and  Forecasting of  Price Volatility: An Application of GARCH and EGARCH Models. Agricultural Economics Research Review. 28 (1) 73-82 DOI: 10.5958/0974-0279.2015.00005.1.

Ajibade, T.B. and Ayinde, O.E. (2020): Food Price Volatility In Nigeria And Its Driving Factors: Evidence From GARCH Estimates. International Journal of Food and Agricultural Economics, ISSN 2147-8988, E-ISSN: 2149-3766  8 (4), 367-380

Antwi, E., Gyamfi, E. N., Kyei, K., Gill, R., & Adam, A. M. (2021): Determinants of Commodity Futures Prices: Decomposition Approach. Mathematical Problems in Engineering. https://doi.org/10.1155/2021/ 6032325

Babihuga, R., & Gelos, G. (2015): Commodity Prices : Their Impact on Inflation in Uruguay Commodity Prices: Their Impact on Inflation in Uruguay (Issue December).

Bevans, R. (2020): Akaike information criterion | when and how to use it (Example). https://www.scribbr.com/statistics/akaike-informationcriter ion/

Bhat, H. S. and Kumar, N. (2010):  On   the    derivation   of   the   Bayesian   Information Criterion, http://nscs00.ucmerced.edu/~nkumar4/Bhat KumarBI C.pdf.

Bollerslev, T. (1986). Generalized autoregressive conditional heteroskedasticity. Journal of econometrics, 31(3), 307-327. https://public.econ.duke.edu/~boller/Published_Papers/joe_86.pdf

Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of the variance of United Kingdom inflation. Econometrica: Journal of the econometric society, 987-1007. https://doi.org/10.2307/1912773

Fameliti, S. P., & Skintzi, V. D. (2022): Statistical and Economic Performance of Combination Methods for Forecasting Crude Oil Price Volatility. Applied Economics, 54, 3031–3054. https://doi.org /10.108 0/ 00036846.2021.2001425

Faraway, J. (1994): Order of actions in regression analysis. In Cheeseman, P and Oldford, W. (Eds.), Selecting Models from Data: Artificial Intelligence and Statistics, 4, 403–411.

Findley, D. F. (1991): Counter-examples to parsimony and BIC. Annals of the Institute of Statistical Mathematics, 43, 505–514.

He, X., and Serra, T. (2022): Are Price Limits Cooling Off Agricultural Futures Markets?  American Journal of Agricultural Economics 1-23. https://doi.org/10.1111/ajae.12306

IGI Global (2023): https://www.igi-global.com/dictionary/sustainable-supply-chain-approach-for-farm-produce-through-hub-chain-model/117442.

Kumari, R. V., Venkatesh, P., Ramakrishna, G., and Sreenivas, A. (2019): Agricultural market intelligence center, a case study of chilli crop price forecasting in Telangana. International Research Journal of Agricultural Economics and Statistics, 10(2), 257–261. https://doi.org/10.15740/has /irjaes/10.2/257-261.

Lestari, E.P., Prajanti, S.D.W., Wibawanto, W. and Adzim, F. (2022): ARCH-GARCH Analysis: An Approach to determine the Price Volatility of Red Chili. AGRARIS: Journal of Agribusiness and Rural Development Research, 8(1), 90-105.

Lim, C.M. and Sek, S.K, (2013): Comparing the performances of GARCH-type models in capturing the stock market volatility in Malaysia. Procedia Economics and Finance 5, 478 – 487. www.elsevier.com/locat e/procedia.

Manasseh, C.O.,  Ogbuabor, J.E. and Obinna, O.K. (2016): Volatility and Commodity Price Dynamics in Nigeria. International Journal of Economics and Financial Issues ISSN: 2146-4138 6(4), 1599-1607, available at http: www.econjournals.com.

National Bureau of Statistics (2022). CPI and Inflation Report November 2022. Retrieved from https://nigerianstat.gov.ng/elibrary/read/1241263. Accessed on May 5, 2024.

Nigatu, G., and Adjemian, M. (2020): A Wavelet Analysis of Price Integration in Major  Agricultural Markets. Journal of Agricultural and Applied Economics, 52(1), 117–134.  https://doi.org/10.1017/aae.2019 .35.

Njagi, H., Waititu, S.G. and Wanjoya, A. (2018): Modelling the Stock Price Volatility Using Asymmetry Garch and Ann-Asymmetry Garch Models. International Journal of Data Science and Analysis; ISSN: 2575-1891, 4(4): 46-52. http://www.sciencepublishinggroup.com/j/ijdsa; doi: 10.11648/j.ijdsa.20180404.11.

Nugroho, A. D., Prasada, I. M. Y., Putri, S. K., Anggrasari, H., & Sari, P. N. (2018): Komparasi Usahatani Cabai Lahan Sawah Lereng Gunung Merapi dengan Lahan Pasir Pantai. AGRARIS: Journal of Agribusiness and Rural Development Research, 4(1). https://doi.org/10.18196/agr. 4156.

Nybo, C. (2020): Sector Volatility Prediction Performance Using GARCH Models and Artificial Neural Network.

Nzeh, I.C., Ogwuru, H.R., Okolie, D.O. & Ibekwe, J. (2023). Applications GARCH models in the volatility of food inflation in Nigeria. Global Journal of Business, Economics, and Management: Current Issues. 13(1), 63-81. https://doi.org/10.18844/gjbem.v13i1.7612

Ogenyi, A.O. and Umeh, J.C. (2019): Determinants of inflation volatility in Nigeria, 1980-2010. AgEcon Search http://ageconsearch.umn.edu

Pilbeam, K., & Langeland, K. N. (2015). Forecasting exchange rate volatility: GARCH models versus implied volatility forecasts. International Economics and Economic Policy, 12, 127-142.

Rauch, E., Spena, P. R., & Matt, D. T. (2019). Axiomatic Design Guidelines for The Design of Flexible and Agile Manufacturing and Assembly Systems For SMEs. International Journal on Interactive Design and Manufacturing, 13, 1–22. https://doi.org/10.1007/s12008-018-0460-1

Von Braun, J., & Tadesse, G. (2012). Global Food Price Volatility and Spikes: An Overview of Costs, Causes, and Solutions. In ZEF- Discussion Papers on Development Policy (Issue 161). https://doi.org/10.22004/ag. econ.120021

Wang, L., Ma, F., Liu, J., & Yang, L. (2019). Forecasting Stock Price Volatility: New Evidence from The GARCH-MIDAS Model. International Journal of Forecasting, 36(2), 684-694. https://doi.org/10.1016 /j.ijforecast.2019.08.005

Yip, P. S., Brooks, R., Do, H. X., & Nguyen, D. K. (2020). Dynamic Volatility Spillover Effects between Oil and Agricultural Products. International Review of Financial Analysis, 69. https://doi.org/10.1016/j.irfa. 2020.101465

Youssef, N. and Rowe, S. (2021): Comparative Study of Modelling and Forecasting Volatility: The Case of Egypt and Japan. International Research Journal of Finance and Economics. ISSN 1450-2887 Issue 182. http://www.internationalresearchjournaloffinanceandeconomics.com

About this Article

Cite this Article

APA

Ogunbona B. D., Osho F. T. & Hairullahi M. U.(2024). Application of Garch, TS-Garch and GJK-Garch Models in Modelling Volatility in Farm Produce Inflation in Nigeria. In K. S. Adegbie, A. A. Akinsemolu, & B. N. Akintewe (Eds.), Exploring STEM frontiers: A festschrift in honour of Dr. F. O. Balogun. SustainE.

Chicago

Ogunbona B. D., Osho F. T. & Hairullahi M. U. 2024. “Application of Garch, TS-Garch and GJK-Garch Models in Modelling Volatility in Farm Produce Inflation in Nigeria.” In Exploring STEM Frontiers: A Festschrift in Honour of Dr. F.O. Balogun, edited by Adegbie K.S., Akinsemolu A.A., and Akintewe B.N., SustainE.

Corresponding Author Email: adisaio@aceondo.edu.ng

Disclaimer: The opinions and statements expressed in this article are the authors’ sole responsibility and do not necessarily reflect the viewpoints of their affiliated organizations, the publisher, the hosted journal, the editors, or the reviewers. Furthermore, any product evaluated in this article or claims made by its manufacturer are not guaranteed or endorsed by the publisher.

Distributed under Creative Commons CC-BY 4.0

Share this article

Use the buttons below to share the article on desired platforms.